DETERMINANTES COU
- Determinante de una matriz cuadrada. Propiedades.
- Dada la matriz
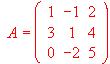 ; Hallar | A | y | A | t .
; Hallar | A | y | A | t .
- Aplicar las propiedades 9 y 10 para transformar el determinante de la matriz
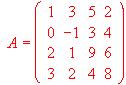 en otro más sencillo de igual valor.
en otro más sencillo de igual valor.
- Obtener, simplificando, el desarrollo de determinante:

- Utilizando las propiedades de los determinantes, resolver la ecuación:

- Utilizando las propiedades de los determinantes, resolver la ecuación:

- Resolver la ecuación
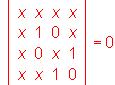
- Dada la matriz
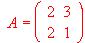 , se llaman "valores propios" de dicha matriz a los valores de l , tales que el determinante de la matriz A - lI sea nulo. Hallar los valores propios de A.
, se llaman "valores propios" de dicha matriz a los valores de l , tales que el determinante de la matriz A - lI sea nulo. Hallar los valores propios de A.
- Dar el concepto de matriz inversa. Calcular la matriz inversa de
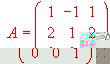
- Dada la matriz
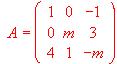 , Averiguar para que valores de m existe A-1 . Calcular A-1 para m = 2.
, Averiguar para que valores de m existe A-1 . Calcular A-1 para m = 2.
- Dada la matriz cuadrada
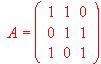 , Estudiar si tiene inversa y en caso afirmativo calcularla. Los vectores
, Estudiar si tiene inversa y en caso afirmativo calcularla. Los vectores 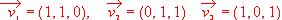 ¿forman una base de R3 ?
¿forman una base de R3 ?
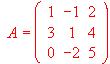 ; Hallar | A | y | A | t .
; Hallar | A | y | A | t .
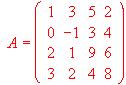 en otro más sencillo de igual valor.
en otro más sencillo de igual valor.



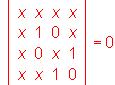
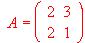 , se llaman "valores propios" de dicha matriz a los valores de l , tales que el determinante de la matriz A - lI sea nulo. Hallar los valores propios de A.
, se llaman "valores propios" de dicha matriz a los valores de l , tales que el determinante de la matriz A - lI sea nulo. Hallar los valores propios de A.
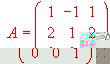
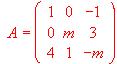 , Averiguar para que valores de m existe A-1 . Calcular A-1 para m = 2.
, Averiguar para que valores de m existe A-1 . Calcular A-1 para m = 2.
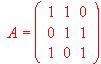 , Estudiar si tiene inversa y en caso afirmativo calcularla. Los vectores
, Estudiar si tiene inversa y en caso afirmativo calcularla. Los vectores 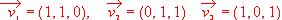 ¿forman una base de R3 ?
¿forman una base de R3 ?