 R} se definen las operaciones:
R} se definen las operaciones:Suma:( x1 , y1 ) + ( x2 , y2 ) = ( x1 + x2 , y1 + y2 ),
 ( x1 , y1 ) , ( x2 , y2 )
( x1 , y1 ) , ( x2 , y2 )  R2.
R2.Producto: t( x1 , y1 ) = ( tx1 ,ty1 ),
 ( x1 , y1 )
( x1 , y1 )  R2 ,
R2 ,  t
t R.
R.Comprobar que (R2 , + ,
 R) es un espacio vectorial
R) es un espacio vectorial
Estudiar si el subconjunto de R3 , W = {(x, y, z), y
 0}, es un subespacio vectorial de R3.
0}, es un subespacio vectorial de R3.
 R3 : x + y = - z} es un subespacio vectorial de R3 .
R3 : x + y = - z} es un subespacio vectorial de R3 .
Determinar los valores de "a" para que resulten linealmente dependientes los vectores (-2, a, a) , (a, -2, a) y (a, a, -2). Obtener en esos casos una relación de dependencia entre los vectores.
Dados los vectores
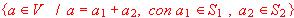
Probar que si los vectores 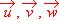 son linealmente independientes, también lo son y1 =
son linealmente independientes, también lo son y1 = 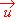 , y2 =
, y2 = 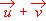 , y3 =
, y3 = 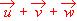
(b) ¿Para que valores de t están alineados los puntos de coordenadas (t, 2, 1 - t) , (2 + t , 1 , - t) , (t , 3 , 1 - t) .
también lo son y1 = x1 , y2 = x1 + x2 , -----------, yn = x1 + x2 + ------ + xn
(b) Para el valor de l obtenido, hallar una relación de dependencia lineal entre esos tres vectores.
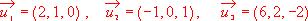 ¿Forman base del espacio vectorial (R3 , +, .) ? ¿Se puede expresar alguno como combinación lineal de los demás?
¿Forman base del espacio vectorial (R3 , +, .) ? ¿Se puede expresar alguno como combinación lineal de los demás?
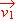 = (1, -3, 2),
= (1, -3, 2), 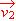 = (0, 4, -1),
= (0, 4, -1), 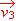 = (2, -14, 6)?
= (2, -14, 6)?
(b) Obtener según los valores de t, la dimensión del subespacio generado por los vectores (l,1,1,1), (2,-l, 2,0), (3,0,3,l) y una base de este subespacio.
(b) Si los vectores v1 , v2 y v3 constituyen una base de R3 , ¿sucede lo mismo con los vectores v1 - v2 ,
- v2 + 2v1 , v3 - v1+ v2 ? ¿Y con v1 + v2 - v3, v1-v2 + v3 , 2v1 +3v2 - 3v3 ?
(b) Si tres vectores e1 , e2 , e3 son linealmente independientes, ¿también lo son los vectores e1 + e2 - 2e3 , e1 + 2e2 - e3 , e1 + 3e2 ? , ¿ y los vectores e1 + e2 , e1 - 2e2 ?