MATRICES COU
- Dadas la matrices
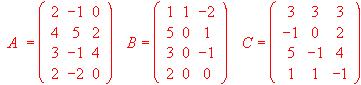 Calcular a) 2A + B, b) B - C, c) 2A + 3C.
Calcular a) 2A + B, b) B - C, c) 2A + 3C.
- Dadas las matrices
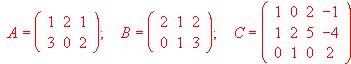 Calcular: (A +B)·C
Calcular: (A +B)·C
- Siendo
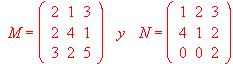 Hallar:
Hallar: 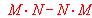
- Encontrar una base del espacio vectorial (M2 , + , R), es decir del espacio vectorial de las matrices cuadradas de orden 2.
- Dadas las matrices
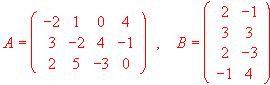 Hallar el producto A · B
Hallar el producto A · B
- Dada la matriz
 Hallar las matrices M, triangular inferior, y N, triangular superior, con nii = 1,
Hallar las matrices M, triangular inferior, y N, triangular superior, con nii = 1,  i
i  {1,2,3}, tales que A= M·N.
{1,2,3}, tales que A= M·N.
- Una cuadrilla de obreros trabaja simultáneamente en la realización de tres obras. Para la primera de ellas necesitan diariamente 100kg de cemento, 235 ladrillos y 44 baldosas; para la segunda necesitan cada día 80kg de cemento, 190 ladrillos y 38 baldosas, y para la tercera obra, las necesidades diarias son de 250kg de cemento, 300 ladrillos y 62 baldosas. Suponiendo que la duración estimada para cada obra sea de 8, 6 y 12 días, respectivamente, se pide expresar matricialmente y calcular las cantidades totales necesarias de cada uno de los materiales empleados en las obras.
-
- Se consideran las matrices
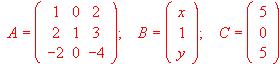 Calcular x, y, z sabiendo que
Calcular x, y, z sabiendo que 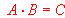
- Resolver la ecuación matricial
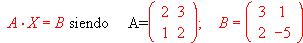
- Resolver la ecuación
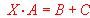 s iendo:
s iendo: 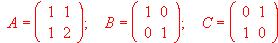
- Dada la matriz cuadrada de orden 2,
 , ver si es regular o singular, intentando calcular su inversa a partir de la definición.
, ver si es regular o singular, intentando calcular su inversa a partir de la definición.
- Concepto de matriz inversa. ¿Es invertible la matriz
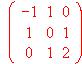 y por qué?
y por qué?
- Aplicar el método de Gauss para calcular el rango de matriz

- Dada la matriz
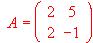 , hallar los valores de a y b para que se verifique la ecuación: A2 + aA + bI = 0, siendo I la matriz identidad.
, hallar los valores de a y b para que se verifique la ecuación: A2 + aA + bI = 0, siendo I la matriz identidad.
- Calcular las potencias sucesivas y la potencia enésima de la matriz
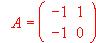
- Sea
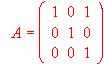 Hallar An , para n
Hallar An , para n 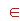 N
N
- Concepto de rango de una matriz. y utilizarlo para determinar si son linealmente independientes los vectores: u1 = (1, 1, 0, 0) , u2 = (0, 1, 1, -1) , u3 = (1, 0, 1, 1) , u4 = (1, 1, 1, 2) .
- Demostrar que el espacio vectorial de las matrices que tienen la forma
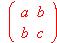 es de dimensión 3.
es de dimensión 3.
- Deteminar las matrices X que conmutan con la matriz
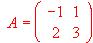 , es decir, tales que AX = XA.
, es decir, tales que AX = XA.
- Dadas las siguientes matrices:
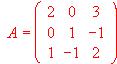 ,
, 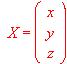 ,
, 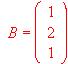 hallar la matriz inversa de A y utilizarla para resolver el sistema de ecuaciones AX = B
hallar la matriz inversa de A y utilizarla para resolver el sistema de ecuaciones AX = B
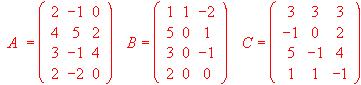 Calcular a) 2A + B, b) B - C, c) 2A + 3C.
Calcular a) 2A + B, b) B - C, c) 2A + 3C.
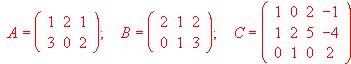 Calcular: (A +B)·C
Calcular: (A +B)·C
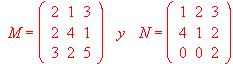 Hallar:
Hallar: 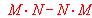
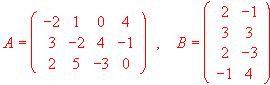 Hallar el producto A · B
Hallar el producto A · B
 Hallar las matrices M, triangular inferior, y N, triangular superior, con nii = 1,
Hallar las matrices M, triangular inferior, y N, triangular superior, con nii = 1,  i
i  {1,2,3}, tales que A= M·N.
{1,2,3}, tales que A= M·N.
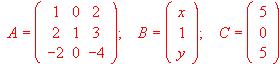 Calcular x, y, z sabiendo que
Calcular x, y, z sabiendo que 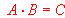
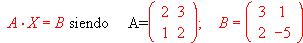
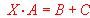 s iendo:
s iendo: 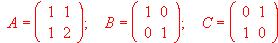
 , ver si es regular o singular, intentando calcular su inversa a partir de la definición.
, ver si es regular o singular, intentando calcular su inversa a partir de la definición.
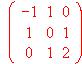 y por qué?
y por qué?

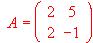 , hallar los valores de a y b para que se verifique la ecuación: A2 + aA + bI = 0, siendo I la matriz identidad.
, hallar los valores de a y b para que se verifique la ecuación: A2 + aA + bI = 0, siendo I la matriz identidad.
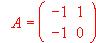
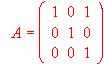 Hallar An , para n
Hallar An , para n 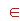 N
N
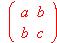 es de dimensión 3.
es de dimensión 3.
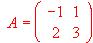 , es decir, tales que AX = XA.
, es decir, tales que AX = XA.
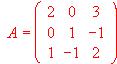 ,
, 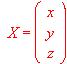 ,
, 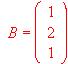 hallar la matriz inversa de A y utilizarla para resolver el sistema de ecuaciones AX = B
hallar la matriz inversa de A y utilizarla para resolver el sistema de ecuaciones AX = B