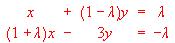- Sea un sistema de tres ecuaciones lineales y tres incógnitas. Discutir todas las posibilidades de compatibilidad e incompatibilidad así como el número de soluciones si éstas existen
- Resolver aplicando el método de gauss el sistema:
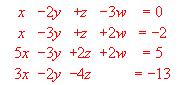Sol (1,2,3,0) - a) Resolver aplicando el método de Gauss y escribir en forma matricial el sistema:
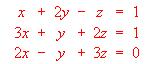
b) Resolverlo también por la regla de Cramer.
- Discutir el siguiente sistema para los distintos valores de "a":
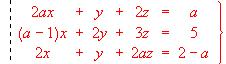
- Discutir y resolver en los casos que proceda el sistema:
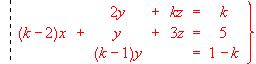
- Resolver y discutir en cada caso el sistema :
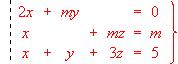
- Hallar el valor de t para que el sistema siguiente sea compatible:
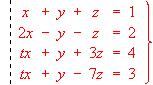
y resolverlo para el valor hallado de t.
- Estudiar, según el valor de t, el sistema:
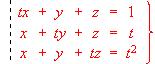
- Estudiar y resolver en función del parámetro "a" el siguiente sistema homogéneo de ecuaciones:
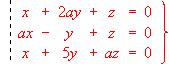
- Condiciones para que un sistema de ecuaciones sea de Cramer. Resolver el sistema
- Resolver la ecuación matricial:
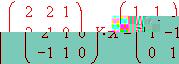
- Enunciar el teorema de Rouché - Frobenius. Estudiar el sistema:
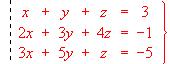
- Discutir para los distintos valores de t y resolver en los casos que sea posible el sistema:
- Enunciar el teorema de Rouché y aplicarlo a la discusión según los posibles valores de t
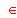R, del sistema de ecuaciones lineales:
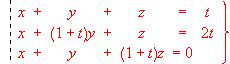
- Estudiar y resolver si ello es posible el sistema:
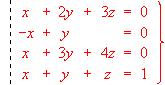
- Consideremos el sistema homogéneo:
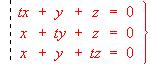
a) Estúdiese según los valores de t.
b) Resuélvase en los casos en que sea compatible. - a) Estudiar según los valores del parámetro "a" el sistema:
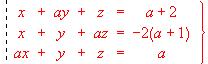
b) Resolverlo por la regla de Cramer en el caso a = -1.
- Estudiar según los valores de "a" y resolver, cuando sea posible, el sistema:
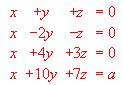
- Discutir y resolver, en los casos en que ello sea posible, según los valores de los parámetros "a" y "b" el sistema siguiente:
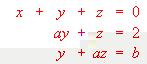
- Analizar y resuelve en su caso, según los valores de los parámetros a y b, el siguiente sistema de ecuacio.es lineales:
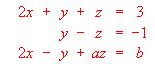
- (a) Estudiar según los valores del parámetro t el sistema
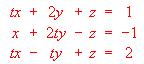
(b) Resolver el sistema anterior cuando éste resulte indeterminado y también en el caso t = 1 (Comprobar que para este valor de t el sistema es compatible y determinado).
- Dadas las matrices
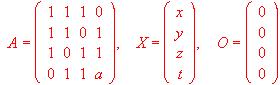
(a) Estudiar según los valores de a el rango de la matriz A.
(b) Resolver la ecuación matricial A · X = O. - (a) Discutir el siguiente sistema de ecuaciones en función de los valores del parámetro a:
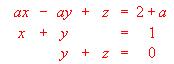
(b) Determinar si el plano
es perpendicular a la recta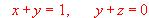 
- Discutir el siguiente sistema de ecuaciones, y resolverlo cuando sea indeterminado:
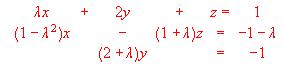
- Discutir según los valores l y resolver cuando sea indeterminado, el sistema de ecuaciones
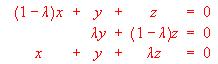
- Enunciar la Regla de Crámer, justificarla razonadamente y aplicarla para resolver el sistema:
.
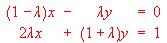
- Enunciar el teorema de Rouché-Frobenius y usarlo para discutir el sistema:
