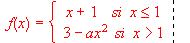
sea continua:
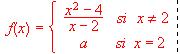 que valor se debe dar al número real a para que la función f(x) sea continua en todo R. Justifiquese.
que valor se debe dar al número real a para que la función f(x) sea continua en todo R. Justifiquese.
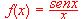 si f(0) = k . ¿Cuánto debe valer k para que la función f(x) sea continua en x = 0?
si f(0) = k . ¿Cuánto debe valer k para que la función f(x) sea continua en x = 0?
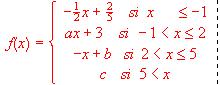
(a)¿resenta la función
(a) Si la derivada de una función f es mayor que 0 en todo punto, probar que no puede haber dos puntos distintos x, y tales que f (x) = f (y). Teniendo en cuenta esto, demostrar que la función
Comprobar que las funciones
Enunciar el teorema del valor medio del calculo diferencial y analizar si puede aplicarse a la función
Calcular,
Calcular,
(b) Calcular
(b) Calcular
(b) Calcular
Sea y = f(x) una función derivable en un punto x0 . Escriba la ecuación de su recta tangente en el punto x0 . Si
 sea continua en el punto x = 0?
sea continua en el punto x = 0?
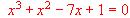 tiene una solución en el intervalo [0, 1].
tiene una solución en el intervalo [0, 1].
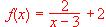 las hipótesis del teorema de Bolzano en el intervalo [2, 4]. Averiguar si se anula en algún punto de (2, 4).
las hipótesis del teorema de Bolzano en el intervalo [2, 4]. Averiguar si se anula en algún punto de (2, 4).
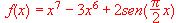 ¿Es cierto que la función f se anula en algún punto x comprendido entre 3 y 4? Enunciar el resultado teórico en el que se basa la respuesta.
¿Es cierto que la función f se anula en algún punto x comprendido entre 3 y 4? Enunciar el resultado teórico en el que se basa la respuesta. 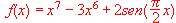 ¿Es cierto que la derivada de la función f se anula en algún punto x comprendido entre 0 y 1? Enunciar el resultado teórico en el que se basa la respuesta.
¿Es cierto que la derivada de la función f se anula en algún punto x comprendido entre 0 y 1? Enunciar el resultado teórico en el que se basa la respuesta.
(b)¿Es derivable en el punto x = 0 la función 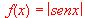 ? Justificar la respuesta.
? Justificar la respuesta.
(b)?Es derivable en el punto x = 1 la función  ? Justificar la respuesta.
? Justificar la respuesta.
(b)?En qué puntos no es derivable la función 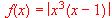 ?
?
 . Calcular los puntos en que la tangente a su gráfica es paralela al eje OX y aquéllos en que es paralela a la bisectriz del primer cuadrante.
. Calcular los puntos en que la tangente a su gráfica es paralela al eje OX y aquéllos en que es paralela a la bisectriz del primer cuadrante.  en que la pendiente de la recta tangente sea máxima.
en que la pendiente de la recta tangente sea máxima. 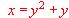 en que la recta tangente sea perpendicular a la recta
en que la recta tangente sea perpendicular a la recta 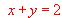 .
. 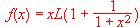 (L = Logaritmo Neperiano).
(L = Logaritmo Neperiano).
(b)? Tiene alguna asíntota esta función?
Determinar los intervalos en los que la función 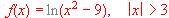 es creciente o decreciente.
es creciente o decreciente.
Encontrar los máximos o mínimos de la función 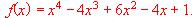
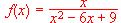 .
.
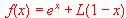 algún extremo en el punto x = 0?.
algún extremo en el punto x = 0?.
(b) Enunciar el resultado teórico en que se basa la respuesta.
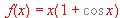
(a) Estudiar si f presenta un máximo o mínimo relativo en el punto x = 
b) ¿tiene alguna asíntota?
(c)?Cuántas veces, cómo mínimo, se anula la derivada de esta función en el intervalo 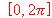 ?
?
Justificar las respuestas. Si éstas se basan en algún resultado teórico, enunciarlo.
(b) Determinar si la función 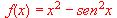 tiene un máximo relativo en x = 0.
tiene un máximo relativo en x = 0. 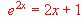 tiene, evidentemente, una solución (x = 0). Demuéstrese que no tiene mas soluciones.
tiene, evidentemente, una solución (x = 0). Demuéstrese que no tiene mas soluciones.
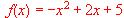 cumple las condiciones del teorema de Rolle en el intervalo
cumple las condiciones del teorema de Rolle en el intervalo 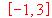 y que efectivamente verifica dicho teorema.
y que efectivamente verifica dicho teorema. 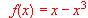 satisface las condiciones del teorema de Rolle en los segmentos [-1, 0] y [0, 1].
satisface las condiciones del teorema de Rolle en los segmentos [-1, 0] y [0, 1]. 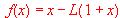 no se anula en el intervalo
no se anula en el intervalo 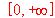 , más que en el punto x = 0.
, más que en el punto x = 0.
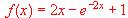 solamente se anula en el punto x = 0.
solamente se anula en el punto x = 0.
(b) Calcular el área de la región limitada por la gráfica de la función anterior el eje X y las rectas verticales x = -1
y x = 1.
(b) Determinar a, b, c para que la función 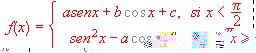 satisfaga la hipótesis del teorema de Rolle en el intervalo
satisfaga la hipótesis del teorema de Rolle en el intervalo 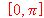
(b) Comprobar si la función 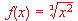 verifica las hipótesis del teorema de Rolle en el intervalo [-1,1]
verifica las hipótesis del teorema de Rolle en el intervalo [-1,1] 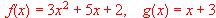 . Aplicar el teorema del valor medio generalizado a esta funciones en el intervalo
. Aplicar el teorema del valor medio generalizado a esta funciones en el intervalo 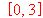 .
.
 cumplen las condiciones del teorema del valor medio generalizado en el intervalo [0, 6] y determinar el punto ó los puntos del interior del intervalo cuya existencia asegura dicho teorema.
cumplen las condiciones del teorema del valor medio generalizado en el intervalo [0, 6] y determinar el punto ó los puntos del interior del intervalo cuya existencia asegura dicho teorema. 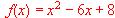 en el intervalo
en el intervalo 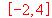 . En caso negativo decir por qué. En caso afirmativo, calcular el punto en el que se verifica el teorema.
. En caso negativo decir por qué. En caso afirmativo, calcular el punto en el que se verifica el teorema. 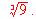
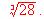


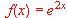 y escribir el término complementario correspondiente.
y escribir el término complementario correspondiente.
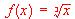 , en un punto adecuado para desarrollar el apartado b).
, en un punto adecuado para desarrollar el apartado b).
b) Hallar un valor aproximado de la raíz cúbica de 9.
c) Acotar el error cometido. 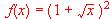 en un entorno del punto x = 4.
en un entorno del punto x = 4.  en el punto
en el punto 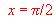 . (ln indica logaritmo neperiano).
. (ln indica logaritmo neperiano).
(b) Calcular 
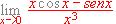 .
. 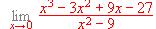
(Hacerlo también descomponiendolo en factores). 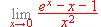
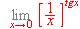
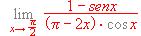 .
. 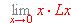 (L = logaritmo neperiano).
(L = logaritmo neperiano).
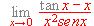 ,
, 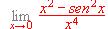 .
.
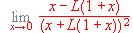 (L = Logaritmo Neperiano).
(L = Logaritmo Neperiano).
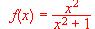 .
.
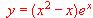 hallése la ecuación de la tangente en un punto de inflexión de la curva.
hallése la ecuación de la tangente en un punto de inflexión de la curva.
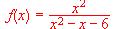 .
. 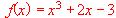 es estrictamente creciente.
es estrictamente creciente.
(b) Hallar el área limitada por la gráfica de la función f, el eje X y las rectas verticales x = 0 y x = 2. 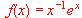 en el intervalo
en el intervalo  .
.