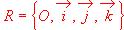 . Hallar las coordenadas del punto medio del segmento AB
. Hallar las coordenadas del punto medio del segmento AB
b) ¿Existe alguna recta que pase por los tres puntos (1, 2, 3) , (2, 4, 1) y (1, 1, 1)
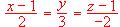


Calcular la ecuación continua de la recta que pasa por el punto P (1, -1, 2) y es perpendicular al plano determinado por los puntos A (1, 0, 1), B (3, 2, 1) y C (2, -1, 0) .
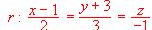
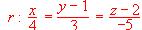 ;
; 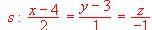
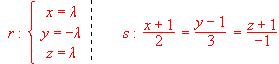
Hallar el plano que las contiene.
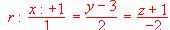 .
.
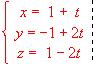
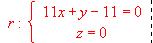 .
.
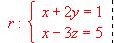
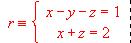
(b) Hallar el área del triángulo ABC, siendo B = (2,-1,3) y C la intersección de r y p.
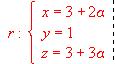 y
y 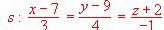
y en caso afirmativo obtener una de sus ecuaciones.
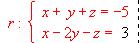 y es paralelo a la recta de ecuación:
y es paralelo a la recta de ecuación: 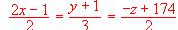

y pasa por el origen de coordenadas.
b) Calcular la distancia entre ese plano y el paralelo a él que pasa por el punto (3,1,1)
(b) Calcular la distancia entre estos dos planos paralelos.
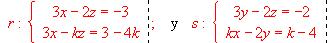
determinar los valores de k para que las rectas r y s estén en un mismo plano y buscar una ecuación de este plano.
b) ¿Cual es la posición de la recta de ecuación
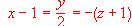 respecto al plano x - y - z - 2 = 0?
respecto al plano x - y - z - 2 = 0?
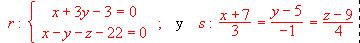
a) ¿Son paralelas?
b) Si la respuesta es si, determinar el plano que las contiene.
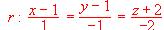 ; y
; y 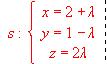
Estudiar su posición y, si fuese posible, calcular la ecuación del plano que las contiene.
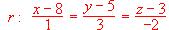 y
y 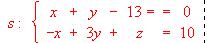
¿Existe alguna recta que corte perpendicularmente a las anteriores? En caso afirmativo hallar una de sus ecuaciones paramétricas
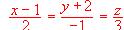
[Volumen de la Pirámide = 1/3 (área de la Base x Altura)].
(a) Calcular la distancia de esta recta al origen. (b) Obtener la ecuación de la recta proyección de r sobre el plano z = 0.
Hállese la distancia entre las recta: 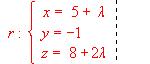 y
y 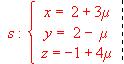
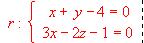 y
y 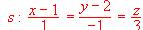
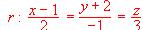 y el plano
y el plano 
Hállese la distancia del punto A(1, 0, -1) al plano
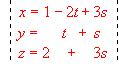
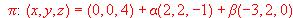 .
.
 y el plano
y el plano 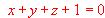 .
.
A (1, 1, 1) , B (0, 1, 0) y C (3, 2, 1).
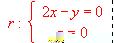 .
.
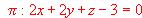 y el punto A (1, 0, 2), sea B el pie de la perpendicular de A a p y C (1, 1, -1) un punto del plano. Se pide el área del triángulo ABC.
y el punto A (1, 0, 2), sea B el pie de la perpendicular de A a p y C (1, 1, -1) un punto del plano. Se pide el área del triángulo ABC.
(b) Calcular el área del triángulo cuyos vértices son los puntos de intersección del plano
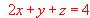
 que pasa por los puntos de coordenadas (0, 0, 3) , (2, 0, -3) , (2, -2, 0).
que pasa por los puntos de coordenadas (0, 0, 3) , (2, 0, -3) , (2, -2, 0).(b) Calcular el área del triángulo que forman los puntos en que el plano
 corta a los tres ejes de coordenadas.
corta a los tres ejes de coordenadas.
(b) Obtener en función de t , el área del triángulo que determinan estos tres puntos.