ALGEBRA COU (mat_2)

  1. Se quieren obtener 10 kg. de pasta de trigo, arroz y maíz, cuyos precios son 20, 40 Y 25 ptas/kg., respectivamente.Hallar la cantidad de cada materia que ha de formar la pasta, sabiendo que el precio resultante ha de ser de 40 ptas/kg. y que la cantidad de arroz ha de ser doble que la de maíz.

  2. Resuelve aplicando el método de Gauss el sistema:

  3. Resolver por el método de Gauss y escribir en forma matricial el siguiente sistema

  4. Escribir en forma matricial y resolver por el método de Gauss, el sistema:

  5. Aplicando el método de Gauss, estudiar el sistema de ecuaciones lineales:

  6. Utilizando el método de Gauss, resolver el sistema de ecuaciones:

  7. Resolver por el método de Gauss el sistema:

  8. ¿Cuántos puntos comunes tienen los planos de ecuaciones:

    ?

  9. Resolver por el método de Gauss el sistema de ecuaciones:

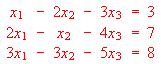
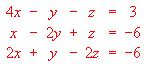
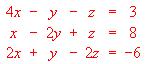
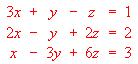
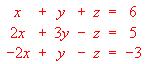
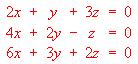
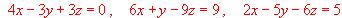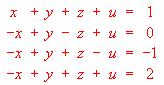
  10. Una empresa cinematográfica dispone de tres cines C1 , C2 , y C3. Cierto día, en cada uno de ellos, proyecta tres películas, P1 , P2 y P3, (P1 en sesión de mañana, P2 en sesión de tarde, y P3 en sesión de noche). El nº de asistentes, (expresado en centenares), a cada una de ellas se indica en la siguiente tabla:

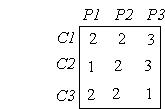
    Sabiendo que los ingresos obtenidos en ese día , en C1 , C2 y C3, fueron de 150000, 140000 y 90000 ptas, respectivamente. Calcular el precio de la entrada para cada una de las tres películas.

  11. Dadas la matrices Calcular (A + B) · C

  12. Siendo Hallar M · N - N · M

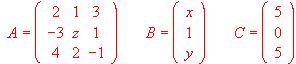  13. Se consideran las matrices Calcular x, y, z, sabiendo que A · B = C

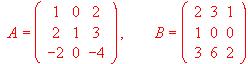  14. Siendo Calcular AxB - BxC.

  15. Obtener los valores de a, b y c, que hacen cierta la relación matricial

  16. Obtener los valores x, y, z, que hacen cierta la siguiente relación matricial.

  17. Obtener los valores x, y, z que hacen cierta la relación matricial:

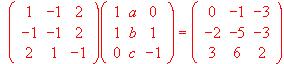
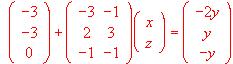
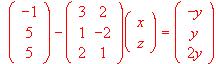
  18. Una marca comercial utiliza tres ingredientes (A, B, y C) en la elaboración de tres tipos de pizzas (P1, P2 y P3). P1 se elabora con 1 unidad de A, 2 de B y 2 de C: P" con 2 unidades de A, 1 de B y 1 de C, y P3 con 2 unidades de A, 1 de B y 2 de C. El precio de venta es de 1.200 ptas.. para P1, 1.025 ptas.. para P2 y 1225 ptas.. para P3. Sabiendo que el margen comercial (beneficio) es de 400 ptas.. en cada una de ellas, ¿qué le cuesta a dicha marca comercial cada unidad de A, B y C? Justificar la respuesta.

  19. En la tabla siguiente se indica la audiencia prevista (en miles de personas) por tres cadenas de televisión (A, B y C) en determinada semana, y en cada uno de los tres segmentos horarios (Mañana, Tarde y Noche)

    A B C
    Mañana 40 60 150
    Tarde 60 50 20
    Noche 150 90 70

    Sin embargo, como consecuencia de la calidad de los programas emitidos, se ha producido en la audiencia prevista (en todos los segmentos horarios) una reducción de un 10% para la cadena A, una reducción de un 5% para la cadena B y un aumento de un 20% para la cadena C. a) Obtener la matriz que expresa la audiencia real obtenida por dichas cadenas de televisión. b) Sabiendo que el beneficio por espectador es de 500 ptas. por la mañana, 700 ptas. por la tarde y 1.000 ptas. por la noche, obtener los beneficios obtenidos por cada una de las tres cadenas.

  20. Una lechería vende leche entera, semidesnatada y desnatada a 100, 120 y 150 ptas el litro, respectivamente. Cierto día vendió 50 litros más de leche entera que de desnatada, y si hubiese vendido 5 litros más de leche desnatada, entonces el número de litros vendidos de leche desnatada sería cuatro veces el de leche semidesnatada vendida. Sabiendo que los ingresos totales obtenidos en dicho día fueron de 26.150 ptas, ¿cuántos litros de cada tipo de leche vendió? b) ¿Cuál sería ese beneficio máximo?

  21. Una marca comercial dispone de tres establecimientos (E1, E2 y E3) en los que prepara cuatro platos combinados (P1, P2, P3 y P4) que vende al precio de 400, 500, 500 y 600 pesetas, respectivamente. Cierto día el número de platos combinados servidos (en cada uno de los establecimientos) es el indicado en la matriz siguiente:

    P1 P2 P3 P4
    E1 C 3 4 B
    E2 A B 5 5
    E3 10 A B 5

    Determinar los valores de A, B y C, sabiendo que los ingresos obtenidos dicho día en E1, E2 y E3, fueron de 7.400, 8.700 y 10.500 pesetas, respectivamente. Justificar la respuesta.