El precio de estacionamiento en cierto garaje es el siguiente :
Obtener la expresión analítica de dicha función.
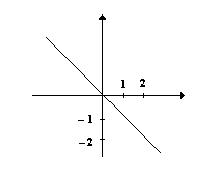
a) ¿cuál es el valor de la derivada de la función en el punto x = -1?
a). Obtener su expresión analítica. b). ¿Cuál de las tres gráficas siguientes correspondería a la función f (x)?. Justificar la respuesta.
a). ¿Qué gráfica entre las tres siguientes es la correspondiente a la función f (x) ?. Justificar la respuesta. b). Determinar la expresión analítica de f(x).
La compañía de transportes que realiza el viaje entre las ciudades A y B, ha comprobado que si el precio del billete es x, (expresado en miles de pesetas), el beneficio mensual obtenido, (en millones de pesetas), viene dado por :
Determinar los valores a, b y c, con objeto de que se cumpla que para x = 1, el beneficio mensual sea de 5 millones, y para x = 3, se obtenga el beneficio mensual máximo de 9 millones. Representar la función obtenida.
Se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 800 pta./m. y la de los otros lados 100 pta./m. Hallar el área del campo de mayor superficie que puede cercarse con 288.000 pta.
Aprovechando como hipotenusa una pared de
a). ¿Para qué valores de x está definida?. b). Estudiar sus puntos de máximo y de mínimo. c). Determinar intervalos de crecimiento e intervalos de decrecimiento.
a). ¿Para qué valores de x está definida? b). Estudiar sus puntos de máximo y de mínimo. c) Determinar intervalos de crecimiento e intervalos de decrecimiento?
20 ptas. la primera hora o fracción
15 ptas. cada siguiente hora o fracción.
100 ptas. el día completo.
Se pide:
a) Importe de un estacionamiento durante 4 horas menos 5 minutos.
b) Dibujar la gráfica de la función que expresa el importe a pagar en función del tiempo de estacionamiento, determinar su dominio y estudiar su continuidad.
- Dos primeras horas, gratis.
- 3 ª hora o fracción, a 40 pta./hora.
- 4ª hora o fracción en adelante, 60 pta./hora hasta un máximo de 6 horas.
Dibujar la gráfica correspondiente a la función que expresa el importe del aparcamiento según el tiempo de aparcamiento. 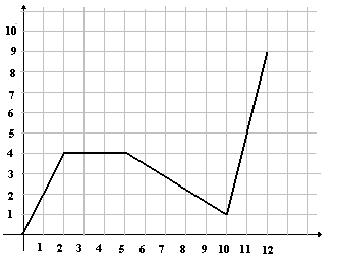
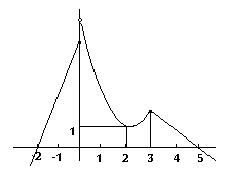
(La parte curva corresponde a una parábola).
b) ¿Cuál es el valor de la derivada de la función en el punto x = 2?
c) ¿Se trata de una función continua en el intervalo.
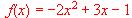 en el punto x 0 = 1.
en el punto x 0 = 1.
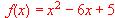 calcular:
calcular:
a) El incremento de la función en el punto x>0 = 3, para un incremento de la variable independiente igual a 0,01.
b) Punto de la gráfica de f (x) en que la tangente tiene por pendiente 2.
c) área limitada por la gráfica de la función y el eje de abcisas. 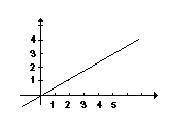
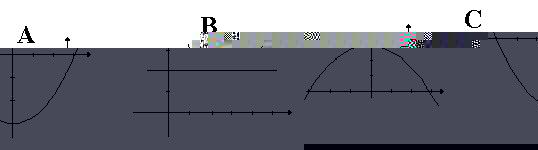
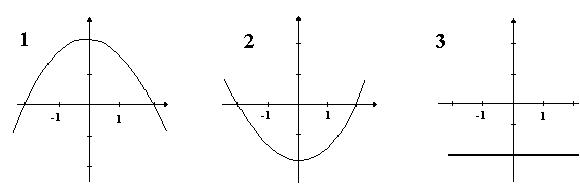
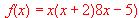
 .
.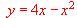 en el intervalo
en el intervalo 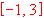 .
.
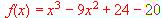
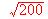 m. se desea acotar una superficie triangular de área máxima. ¿Que medidas deberán tener los otros dos lados, (catetos) ?
m. se desea acotar una superficie triangular de área máxima. ¿Que medidas deberán tener los otros dos lados, (catetos) ? 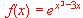
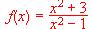

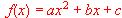 , pase por el punto (4 , 6) y tenga su valor mínimo en el punto (2, -2).
, pase por el punto (4 , 6) y tenga su valor mínimo en el punto (2, -2). 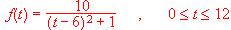
 (t denota la hora del día)
(t denota la hora del día)
Sabiendo que abre sus puertas con cero visitantes y que la afluencia máxima se produce a las 12 horas con 900 visitantes, se pide: a) Determinar los coeficientes A, B y C. b) Representar la función.
Un parque de atracciones ofrece, a grupos de 10 escolares, una entrada de 1.000 ptas por escolar. Además les hace un descuento de 50 ptas a cada uno por cada nuevo escolar que incorporen al grupo (hasta un máximo de diez incorporaciones) a) ¿Qué número de escolares por grupo hará máximo el beneficio de dicho parque de atracciones? b) ¿Cuál sería ese beneficio máximo?

Sabiendo que es una función continua y que a las 15 horas se alcanza el consumo máximo de 40 millares de litros:
a) Determinar, justificando la respuesta, los valores de A, B y C.
b) Representar dicha función.