| Nº Caries | f. Absoluta | f. Relativa |
| 0 | 25 | 0,25 |
| 1 | 20 | 0,2 |
| 2 | x | z |
| 3 | 15 | 0,15 |
| 4 | y | 0,05 |
a)Completa la tabla obteniendo los valores x, y, z.
b) Hacer un diagrama de sectores.
c) Calcular el nº medio de caries.

a) Completar la tabla con las frecuencias absolutas y las frecuencias relativas que faltan. Justificar la respuesta.
b) A través de un diagrama de barras ó un diagrama de sectores, representar gráficamente dicha información.
| Número de hijos | Frecuencia absoluta | Frecuencia relativa |
| 0 | .... | 0,2 |
| 1 | 15 | .... |
| 2 | .... | .... |
| 3 | 5 | .... |
| 4 | 4 | .... |
| 5 | .... | .... |
a) Completar la tabla con las frecuencias absolutas y las frecuencias relativas que faltan.
b) Calcular el número medio de hijos por familia.
c) ¿Qué porcentaje de familias tienen 3 o más hijos?
| Número de puntos | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 |
| Repeticiones | ? | 32,00 | 35,00 | 33,00 | ? | 35,0 |
Determina las frecuencias que faltan sabiendo que la puntuación media es 3,6. Calcula la mediana y la moda.
a) Determinar la mediana.
b) ¿Qué porcentaje de alumnos tiene nota inferior a 32?
| Número de caries | 0 | 1 | 2 | 3 | 4 |
| Frecuencia Absoluta | 5 | 15 | 60 | 18 | 2 |
a) Hacer una representación gráfica a través del Diagrama de barras o el Diagrama de sectores.
b) Obtener el número medio de caries y la desviación típica.
c) ¿Qué porcentaje de escolares tienen 2 o más caries? Justificar las respuestas.
A un grupo de 100 personas se les mide la estatura (con el mismo aparato de medida), resultando una estatura media de 165 cm, una estatura mediana de 167 cm, y una desviación típica de 15,6 cm. Una vez obtenidos estos valores, se detecta en el aparato de medida un error sistemático por defecto de 1 cm (es decir la estatura de cada persona es en realidad 1 cm más de lo que se ha observado). Teniendo en cuenta esta información: a) ¿Cuáles serían los valores correctos para la estatura media, estatura mediana y desviación típica, en ese grupo de personas? Justificar la respuesta. b) Interpretar los resultados.
La calificación media en Matemáticas obtenida en cierto grupo de alumnos ha sido 5,5, la mediana 6 y la desviación típica 0,8. Una vez calificados los exámenes el profesor detecta un error en la redacción de un problema y decide subir 0,5 puntos la calificación de cada alumno. a) ¿Cuáles serían los valores correctos para la calificación media, mediana y desviación típica en ese grupo de alumnos?. Razonar la respuesta. b) Interpretar el significado del valor obtenido para la mediana. c) A partir de los datos correctos, obtener e interpretar el coeficiente de variación.
| xi | 13 | 17 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 |
| fi | 1 | 2 | 3 | 5 | 4 | 4 | 8 | 6 | 2 | 1 |
| Calific. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Nº alumnos | 1 | 3 | 3 | 0 | 5 | 8 | 9 | 7 | 2 | 1 | 1 |
Hallar la media, mediana, moda, varianza y desviación típica de la distribución.
 |
a) Sin agrupar los datos en clases o intervalos, halla la media, moda, mediana, cuartil inferior (primero) y superior (tercero), así como la desviación típica.
b) Comprueba si en el intervalo 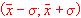 se encuentran aproximadamente el 68 % de los datos.
se encuentran aproximadamente el 68 % de los datos.
c) Agrupa los datos en intervalos de amplitud 11 y halla los valores más representativos de la moda, mediana y cuartiles inferior y superior. ¿Qué diferencias se aprecian con la solución verdadera?
d) Dibuja el Histograma correspondiente.
| Intervalos | [0, 2) | [2, 4) | [4, 6) | [6, 8) | [8, 10) |
| Nº alum. | 2 | 4 | 8 | 5 | 1 |
Hallar la media, mediana, moda, varianza y desviación típica de la distribución
| Número de infartos | 0 | 1 | 2 | 3 | 4 |
| Frecuencias Absolutas | 10 | 20 | 32 | 24 | 14 |
a) Calcular el número medio de infartos atendidos diariamente.
b) Calcular la varianza y la desviación típica.
| Grupo 1: | 22 | 18 | 20 | 21 | 19 |
| Grupo 2: | 31 | 29 | 30 | 32 | 28 |
| Grupo 2: | 25 | 15 | 20 | 30 | 10 |
Contestar justificando la respuesta:
a) ¿Qué característica (centralización o dispersión) hace diferentes a los datos correspondientes a los grupos 1 y 2? ¿Qué medida (ó valor típico) podríamos utilizar para representar dicha característica? Calcularla en ambos conjuntos.
b) ¿Qué característica (centralización ó dispersión) hace diferentes a los datos correspondiente a los grupos 1 y 3? ¿Qué medida (ó valor típico) podríamos utilizar para representar dicha característica? Calcularla en ambos conjuntos.
y = 0,6 x + 8
Sabiendo que la media y la desviación típica de la distribución marginal de la variable x son iguales a 12,2 y 1,3 , respectivamente, calcular :
a) La media de la variable y
b) La covarianza.
Un conjunto de datos bidimensionales (x,y) tiene coeficiente de correlación r = 0,8 y las medias de las distribuciones marginales son 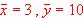 . Sin efectuar cálculos, razona por qué las siguientes ecuaciones no pueden corresponder a la recta de regresión de y sobre x
. Sin efectuar cálculos, razona por qué las siguientes ecuaciones no pueden corresponder a la recta de regresión de y sobre x
| C.O.U. | 6,8 | 8,2 | 7,4 | 6,6 | 7,8 |
| Slectividad | 6,2 | 7 | 7,6 | 5 | 5,4 |
a) Calcular el coeficiente de correlación y la ecuación de la recta de regresión de las calificaciones en la Selectividad respecto de las calificaciones en C.O.U.
b) Obtener la calificación en la Selectividad que resulta previsible para un alumno cuya calificación en C.O.U: fue 7.
| Padres | 165 | 163 | 167 | 180 | 175 |
| Hijos | 168 | 166 | 170 | 175 | 178 |
Representar el diagrama de dispersión y calcular el coeficiente de correlación.
Dibuja posteriormente la nube de puntos.
| Precio (x) | 40 | 60 | 70 | 90 | 100 |
| Unidades (y) | 20 | 15 | 12 | 8 | 2 |
Se pide
a) Dibujar el correspondiente diagrama de puntos.
b) Calcular el coeficiente de correlación.
c) Obtener la pendiente de la recta de regresión e interpretar su signo.
| Dia xi | 2 | 5 | 8 | 11 | 14 | 15 |
| Peso yi | 400 | 300 | 500 | 900 | 800 | 1.100 |
a) Dibujar el diagrama de dispersión
b) Obtener la recta de regresión y dibujarla.
| X | 9 | 5 | 4 | 9 | 8 | 10 | 1 | 4 | 3 | 7 |
| Y | 6 | 5 | 3 | 7 | 6 | 8 | 2 | 4 | 4 | 6 |
a) Calcular el coeficiente de correlación lineal.
b) Obtener la recta de regresión de Y sobre X.
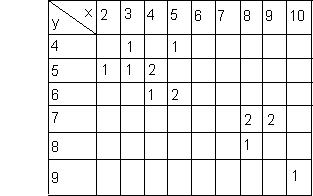
Hallar la recta de regresión de y sobre x. ¿Cuál será la nota esperada de música correspondiente a 6 en matemáticas?
| Edad | 9 | 6 | 7 | 8 | 7 | 4 | 2 | 3 | 2 | 1 |
| Conducta agrsiva | 6 | 6.4 | 6.7 | 7 | 7.4 | 7.9 | 8 | 8.2 | 8.5 | 8.9 |
a) Obtener la recta de regresión de la conducta agresiva en función de la edad.
b) A partir de dicha recta, obtener el valor de conducta agresiva que correspondería a un niño de 7 años.
| Tiempo | 1 | 3 | 5 | 6 | 8 |
| Peso | 10 | 15 | 25 | 40 | 60 |
a) Calcular el coeficiente de correlación lineal.
b) Obtener la recta de regresión lineal del Peso en función del tiempo
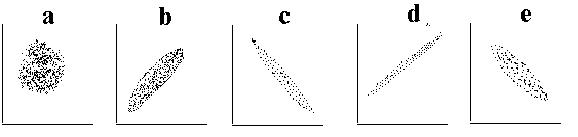
Identificar (justificando la respuesta) la nube de puntos correspondiente a cada uno de ellos.
Una compañía de seguros considera que el número de vehículos (Y) que circulan por la autopista Vasco-Aragonesa puede ponerse en función de accidentes (X) que ocurren en ella. Durante 5 días obtuvo los siguientes resultados:
| x | 5,00 | 7,00 | 2,00 | 1,00 | 9,00 |
| y (miles de coches) | 15,00 | 18,00 | 10,00 | 8,00 | 20,00 |
(a) Calcula el coeficiente de correlación lineal.
(b) Si ayer se produjeron seis accidentes ¿cuántos vehículos podemos suponer que circulaban por la autopista?
(c) ¿Es buena esta predicción? Razona la respuesta.
(d) Dibuja el diagrama de dispersión.
Los 50 alumnos del COU de cierto Instituto han obtenido una calificación media de 5,4 en Filosofía y una calificación media de 5,5 en Lengua Española.
a) Obtener la recta de regresión que expresa la calificación de Filosofía en función de la calificación en Lengua Española, sabiendo que pasa por el punto (0,1).
b) ¿Qué calificación en Filosofía debería obtener un alumno que tiene un 7 en Lengua Española?
a) Obtener el coeficiente de correlación lineal entre Gastos e Ingresos
Gastos
4
2 8 5
3
Ingresos
6,5
5
3,5
7
4,5
b) Interpretar el signo de dicho coeficiente.
c) Obtener la recta de regresión de los ingresos en función de los gastos.