| Año | 1982 | 1984 | 1986 | 1988 |
| Lluvia | 630 | 510 | 540 | 310 |
Hallar la previsión de lluvias para el año 1989 utilizando el polinomio de interpolación de segundo grado más idóneo.
| Años | Población |
| 1960 | 1,050 |
| 1970 | 1,290 |
| 1980 | 1,552 |
Estimar la población en el año 1976 mediante:
a) Interpolación lineal
b) Interpolación cuadrática.
| Año | 1 | 2 | 3 |
| P.I.B. (miles de millones de ptas.) | 740 | 2580 | 5900 |
De seguir la misma tendencia, ¿qué P.I.B. se puede prever mediante interpolación cuadrática para el cuarto año?
| Años | Ventas |
| 1977 | 15 |
| 1980 | 20 |
| 1983 | 28 |
| 1986 | 40 |
Se pide : a) Determinar la función definida a trozos que daría por interpolación lineal las ventas en los años intermedios y utilizarla para calcular las ventas en 1978.
b) Efectuar la previsión de ventas para 1989 utilizando el polinomio de interpolación de segundo grado a partir de los datos correspondiente a los años 1980, 1983 y 1986.
| Años | 1983 | 1984 | 1985 | 1986 | 1987 |
| Beneficios | 1.100 | 1.300 | 1.600 | 2.100 | 2.900 |
Se pide : a) Determinar el polinomio de interpolación de segundo grado correspondiente a los datos de 1983, 1985 y 1987. b) Obtener los valores teóricos de los beneficios en 1984 y 1986 utilizando el polinomio anterior.
: a) Hallar la función lineal que expresa el coste del billete en función de los Km. recorridos.
b) Calcular por extrapolación, el precio del billete, cuando la distancia recorrida sea de 500 Km.
c) Si el billete cuesta 400 pta. ¿Cuántos Km. tiene el recorrido?
| x | 6,00 | 8,00 | 13,00 | 16,00 |
| f (x) | 225,00 | 400,00 | 1040,00 | 1600,00 |
a) Representar los valores y expresar la función definida a trozos.
b) Hallar por interpolación lineal la máxima carga para un eslabón de 10 mm.
c) Hallar la máxima carga para un eslabón de 20 mm. utilizando el polinomio de interpolación de segundo grado a partir de los datos de 8, 13 y 16 mm.
.
| Año | 1977,00 | 1980,00 | 1983,00 | 1986,00 |
| Ventas | 15,00 | 20,00 | 28,00 | 40,00 |
Se pide :
a) Representar los valores y expresar la función definida a trozos.
b) Hallar por interpolación lineal las ventas en el año 1978.
c) Hallar la previsión de ventas para 1989 utilizando el polinomio de interpolación de segundo grado a partir de los datos de 1980, 1983 y 1986.
| Año | 1985,00 | 1987,00 | 1988,00 | 1989,00 |
| Espera | 15,00 | 20,00 | 28,00 | 40,00 |
a) Por interpolación lineal, calcular el número de personas que esperaban teléfono en el año 1986 a partir de los datos de 1985 y 1987.
b) Haced una previsión para el año 1990 mediante interpolación cuadrática a partir de los datos de 1987, 1988 y 1989.
En un test psicológico de 40 pruebas, aplicando a niños de diferentes edades, se observa que los fallos disminuyen a medida que los niños son mayores, según la tabla:
| Edad | 4,00 | 6,00 | 8,00 | 10,00 |
| Fallos | 17,00 | 15,00 | 13,00 | 11,00 |
a) Hallar por interpolación lineal los fallos de un niño de 5 años de edad.
b) Hallar los fallos de un niño de 9 años, utilizando el polinomio de interpolación de segundo grado, a partir de los datos de los niños de edades 6, 8 y 10.
.
| Años | 1970,00 | 1975,00 | 1980,00 | 1985,00 |
| Millones de turistas | 24,10 | 30,10 | 38,10 | 43,20 |
a) Hallar la previsión para 1988 a partir de la función lineal del último trozo 1980 - 1985.
b) Efectuar la misma previsión con el polinomio de interpolación de 2º grado a partir de los datos de 1975, 1980 y 1985. .
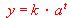
donde t representa los días transcurridos desde el inicio del experimento e y el número de moscas que forman la población. Para t = 10 días, resulta y = 1219 moscas; para t = 20 días, y = 1486. ¿Cual será el número de moscas cuando el valor de t sea de 30 días?
| x | 1 | 3 | 5 |
| y | 7 | 21 | 43 |
Determinar la función cuadrática que pasa por estos puntos. Calcular el valor aproximado de y para x = 2.
| Tiempo | 3 | 5 | 8 |
| Peso | 8 | 22 | 73 |
a). Obtener el polinomio de interpolación de 2º grado correspondiente.
b). Determinar a partir de dicho polinomio el peso que correspondería a un embrión de 6,5 días.
| Gastos en publicidad | 2 | 5 | 10 |
| Ingresos por ventas | 10 | 16 | 106 |
a) Obtener el polinomio de interpolación de 2º grado que expresa los ingresos en función de los gastos.
b) ¿Qué ingresos debería obtener esa marca en un mes en el que ha invertido 7 millones de ptas. en publicidad?
| 1994 | 1995 | 1996 | |
| Gastos de Producción | 3 | 4,5 | 7 |
| Ingresos por ventas | 10 | 13 | 20 |
a) Obtener el polinomio de interpolación de 2º grado que expresa los ingresos por ventas en función de los g!stos de producción.
b) ¿Qué ingresos cabe esperar obtenga la editorial en 1997 si los gastos de producción estimados son de 6.000 millones de pesetas?