Un fabricante de alfombras dispone de las siguientes existencias de lana: 500 kg. de color azul , 400 kg. de color verde y 225 kg. de color rojo. Desea fabricar alfombras de dos tipos que llamaremos A y B. Las del tipo A llevan 1 kg. de lana azul, y 2 kg. de lana verde. Las del tipo B, 2 kg. de lana azul, 1 kg. de verde y 1 kg. de lana roja. Por cada alfombra del tipo A obtiene un beneficio de 2.000 ptas. y 3.000 por cada una del tipo B. ¿Cuántas alfombras debe fabricar de cada clase para que la ganancia sea máxima?
En una fábrica de dulces se producen dos tipos de pasteles. Uno de ellos lleva 2 huevos, 50 gr. de harina y 20 gr. de azúcar. El otro tipo lleva 2 huevos, 40 gr. de harina y 25 gr. de azúcar. Si se dispone de 15 kg. de harina, 7 kg. de azúcar y 50 docenas de huevos, y el fabricante ha de servir al menos 100 pasteles del primer tipo y 150 del segundo, se pide:
Calcular el número de pasteles que deben producirse de cada clase para que, siendo 12 ptas. el beneficio que produce cada pastel del primer tipo y 10 las del segundo, el beneficio sea máximo.
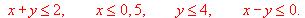
Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas. El fabricante dispone para la confección de 750 m 2 de tejido de algodón y 1000 m2 de tejido sintético. Cada pantalón precisa de 1 m 2 de algodón y 2 m 2 de tejido sintético, y cada chaqueta de 1'5 m 2 de algodón y 1 m2 de tejido sintético.
Si el precio de venta del pantalón es de 5.000 ptas. y el de la chaqueta 4.000 ptas. ¿cuántos pantalones y chaquetas debe suministrar el fabricante para que el importe de la venta sea máximo?
En una urbanización se va a construir casas de dos tipos, A y B. La empresa constructora dispone de 300 millones de ptas. siendo el coste de las casas del tipo A de 6,5 millones de ptas. y el de las del tipo B, 4 millones. Además las casa del tipo A han de ser al menos el 40% del total y las del tipo B, al menos el 20%.
Determinar cuántas casas hay que fabricar de cada tipo para que, siendo 1,5 millones de ptas. el beneficio producido por cada casa tipo A, y 1 millón el proporcionado por las del tipo B, el beneficio se máximo.
Dos abonos A y B, están compuestos por los tres mismos componentes: P, Q y R, aunque en distinta proporción. El abono tipo A, cuyo precio es de 12 ptas/kg. consta de 2 unidades de P, 2 de Q y 1 de R; el abono tipo B, cuyo precio es de 15 ptas./kg. consta de 1 unidad de P, 2 de Q y 2 de R.
Si el abono necesario para determinada plantación es de 8, 10 y 6 unidades de P, q y R, respectivamente, ¿cuál es la combinación de los abonos tipo A y B que supone un coste mínimo?
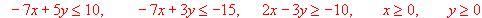
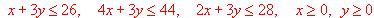
Una fábrica de muebles tiene almacenada de 1.200 m3 de madera de ébano y 1500 m3 de madera de pino, con los cuales fabrica dos clases de muebles, A y B. En la fabricación de los muebles del tipo A utiliza 1 m3 de ébano y 3 m3 de pino; en la de los del tipo B utiliza 3 m3 de ébano y 2 m3 de pino. Si el precio de venta de los muebles tipo A y B es de 50.000 y 60.000 ptas. respectivamente, calcular el número de muebles que han de fabricarse de cada tipo para que el importe de la venta sea el máximo posible.
Una empresa fabrica dos tipos de televisores: en color y en blanco y negro. Todos ellos han de pasar por los departamentos de electrónica y de montaje; cada departamento dispone semanalmente de 100 horas. Un televisor en color necesita 3 horas en el departamento de electrónica y de 1 hora en el de montaje, mientras que uno en blanco y negro requiere 1 y 2 horas respectivamente. ¿Qué cantidad de televisores de cada tipo han de fabricarse semanalmente para que, siendo el beneficio que produce uno de color de 5.000 pta. y uno de blanco y negro 4.000 pta. el beneficio sea máximo?
Una empresa fabrica dos clases de lápices. De la clase A a 20 pta. unidad y de la clase B a 15 pta. unidad. En la producción diaria se sabe que: el número de la clase B no supera en 1.000 unidades a los de A; entre las dos clases no superan a 3.000 unidades y los de la clase B no bajan de 1.000 unidades. Hallar el costo máximo y mínimo de la producción diaria.
Cierto laboratorio ha sido informado de que ha de proporcionar como mezcla para la fabricación de un producto H, dos materias primas A Y B. De A debe poner 40 mg. y de B 45 mg. Se pone en contacto con un fabricante que le ha ofrece dos tipos de producto H, cuyas características son:
Producto H2 : 10 mg. de A 5 mg. de B 50 pta./mg.
.
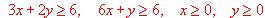
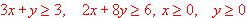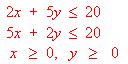
hallar la que maximiza la función objetivo z = 2x + 7y.
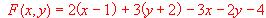, sujeta a las restricciones :
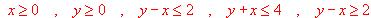
Una ganadería desea proporcionar a su ganado una dieta que contenga un mínimo de 24 unidades del pienso A y un mínimo de 25 unidades del pienso B. En el mercado se comercializan dos tipos de compuestos C1 y C2, elaborados con ambos piensos. El paquete de C1 contiene 1 unidad de A y 5 de B, siendo su precio 100 ptas. y el de C2 contiene 4 unidades de A y 1 de B, siendo su precio 300 ptas. ¿Que cantidades de C1 y de C2 deberá emplear la ganadería para preparar su dieta con el mínimo coste.?
Una empresa textil confecciona dos tipos de camisetas, A y B. El tiempo requerido para la confección de una camiseta tipo A es el doble que para una del tipo B. Teniendo en cuenta el número de operarios de que dispone, se sabe que si únicamente confeccionara camisetas del tipo B, podría hacer 1000 en un día. El suministro de material para determinado mes, sólo hace posible la confección de 800 camisetas diarias, (incluyendo ambos tipos). Determinar el número de camisetas de cada tipo que han de confeccionarse diariamente durante dicho mes con objeto de obtener máximo beneficio, sabiendo que cada camiseta tipo A vendida reporta una ganancia de 200 ptas. y cada camiseta tipo B, 150 ptas.
Una marca comercial prepara dos tipos de pintura (P1 y P2). El bote P1 contiene 1 Kg. de la sustancia A, 2 Kg. de la B y 1 Kg. de la C y el bote de P2 contiene 2 Kg. de A y 1 Kg. de B. La marca comercial dispone en su almacén de 4.000 Kg. de A, 5.000 Kg. de B y 3.000 Kg. de C. Sabiendo que por cada bote de P1 obtiene una ganancia de 200 ptas. y por cada bote de P2, 300 ptas. ¿cuántos botes de cada tipo deberá preparar con objeto de obtener máximo beneficio? Justificar la respuesta.
Un laboratorio utiliza las sustancias A y B en la elaboración de dos vacunas. La primera se prepara con 2 unidades de A y 1 de B, siendo su precio 3000 ptas. y la segunda se elabora con 2 unidades de A y 3 de B, siendo su precio 4000 ptas. Sabiendo que dicho laboratorio dispone de un total de 400 unidades de A y 300 de B, ¿cuántas vacunas de cada tipo deberá preparar para obtener el máximo beneficio?
Una empresa construye en dos factorías (F1 y F2) tres tipos de barcos deportivos (A, B y C). La factoría F1 construye en 1 mes: 1 barco tipo A, 5 tipo B y 1 tipo C, siendo su coste de mantenimiento mensual 6 millones de ptas. y F2 construye en un mes: 1 barco tipo A, 1 tipo B y 2 tipo C, siendo su coste mensual 3 millones de ptas. La empresa se ha comprometido a entregar anualmente a cierto club náutico, 3 barcos tipo A, 15 tipo B y 12 tipo C. ¿Cuántos meses al año deberá trabajar cada factoría con objeto de que la empresa cumpla su compromiso con el mínimo coste? Justificar la respuesta.
Un comerciante acude a cierto mercado a comprar naranjas con 50.000 ptas. Le ofrecen dos tipos de naranjas: las de tipo A a 50 ptas.. el kg y las de tipo B a 80 ptas.. el kg. Sabiendo que sólo dispone en su furgoneta de espacio para transportar 700 kg de naranjas como máximo y que piensa vender el kg de naranja tipo A a 58 ptas.. y el kg de tipo B a 90 ptas.. contestar justificando la respuestas: a) ¿Cuántos kg de naranjas de cada tipo deberá comprar para obtener máximo beneficio? b) ¿cuál seria ese beneficio máximo?
Una empresa produce dos tipos de componentes eléctricas (A y B). El tiempo requerido para la fabricación de la componente A es el doble que para la B, y es conocido que si únicamente fabricara componentes tipo B podría hacer un máximo de 5.000 al día. El suministro de material para cierto mes hace posible, como máximo, la fabricación de 4.00 componentes diarias (incluyendo ambos tipos). Sabiendo que los márgenes comerciales (beneficios) son de 200 ptas.. por cada componente tipo A y de 150 ptas. por cada componente de tipo B, contestar justificando la respuesta: a) ¿Cuántas componentes de cada tipo deberá fabricar diariamente durante dicho mes con objeto de maximizar su beneficio? b) ¿Cuál sería el beneficio máximo?
Para la desinfección de cierta piscina es necesario un mínimo de 24 litros del producto A y un mínimo de 25 litros del producto B. En el mercado se comercializan dos preparados (P1 y P2 ) al precio de 1.000 y 3.000 pesetas el litro, respectivamente. En la composición de P1 hay un 10% de A y un 50% de B, y en la de P2, un 40% de A y un 10% de B.
Determinar, justificando la respuesta: a) ¿Cuántos litros de P1 y de P2 tendremos que utilizar para desinfectar la piscina con el coste mínimo? b) ¿Cuál será el coste mínimo?