ALGEBRA LOGSE

  1. (1) Define lo que son vectores linealmente independientes en (2) Prueba que los vectores u = (2 , -1 ,0) y

    v = (1 , 0 , 1) son linealmente independientes.

    (3) Halla el valor de t para el cual el vector w = (8 , -5 , t) depende linealmente de u y v

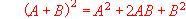  2. (1) [1 PUNTO]. Si A y B son dos matrices y del mismo orden; ¿es cierta en general la relación

    ? Justifica la respuesta.

    (2) [1'5 PUNTO]. Calcula, según los valores de a, el rango de la matriz

    .

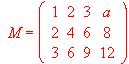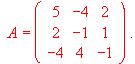  3. Sea A la matriz (1) Comprueba que se verifica 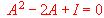, siendo I la matriz identidad de orden 3.

    (2) Usando la igualdad anterior, calcula razonadamente

  4. Sabiendo que la matriz A verifica la relación resuelve el sistema

  5. Del sistema de ecuaciones se conocen todas sus soluciones, que son 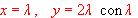variando en los números reales. También se sabe que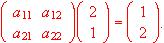

    Resuelve el sistema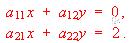

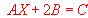  6. Resuelve la ecuación matricial , siendo

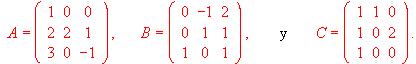
  7. (1) Define el concepto de matriz inversa de una matriz cuadrada.

    (2) ¿Qué condición debe cumplir el determinante de una matriz cuadrada para que ésta sea invertible?

    (3) Estudia si hay algún valor de a para el que la siguiente matriz tiene inversa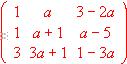

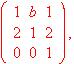  8. (1) Dada la matriz A = ¿para qué valores del parámetro b no tiene inversa A? Justifica la respuesta.

    (2) Si existe, calcula la inversa de A para b = -1.

  9. De las matrices Se sabe que .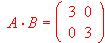

    (1) ¿Tiene A inversa? Justifica la respuesta y si la respuesta es afirmativa indica cuál es la inversa de A?

    (2) ¿Es cierto que A· B = B · A en este caso?

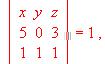  10. Sabiendo que Calcula de forma razonada el valor de los siguientes determinantes sin desarrollarlos:

  11. Sin desarrollar el determinante, demuestra que

  12. Resuelve la ecuación

  13. Sea A la matriz de los coeficientes del sistema de ecuaciones

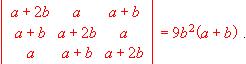
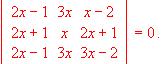
    Resuelve el sistema sabiendo que 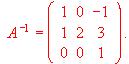(1997)

  14. Una fábrica de electrodomésticos tiene una producción semanal fija de 42 unidades. La fábrica abastece a tres establecimientos - digamos A, B y C - que demandan toda su producción. En una determinada semana el establecimiento A solicitó tantas unidades como B y C juntos y, por otro lado, B solicitó un 20% más que la suma de la mitad de lo que pidió A mas la tercera parte de lo que pidió C. ¿Cuántas unidades solicitó cada establecimiento dicha semana?

  15. Escribe, cuando sea posible, sistemas de ecuaciones que respondan a las característica siguientes:
    (1) Un sistema de tres ecuaciones con dos incógnitas que tengan infinitas soluciones. (2) Un sistema de dos ecuaciones con tres incógnitas que sea compatible y determinado.
    (3) Un sistema de tres ecuaciones con tres incógnitas que no tenga ninguna solución.
    (4) Un sistema de tres ecuaciones con tres incógnitas que tenga solución única.
    Razona, en cada caso, tu respuesta.

  16. Considera el sistema de ecuaciones
    (1) [0'75 PUNTOS]. ¿Existe una solución del mismo en la que y = 0?
    (2) [0'75 PUNTOS]. Resuelve el sistema homogéneo asociado al sistema dado.
    (3) [1 PUNTO]. Haz una interpretación geométrica tanto del sistema dado como de sus soluciones.

  17. Considera la matriz

    donde a, b y c son no nulos.
    (1) [1 punto]. Determina el número de columnas de A que son linealmente independientes.
    (2) [1'5 puntos]. Calcula el rango de A y razona si dicha matriz tiene inversa.

    <,i>[2'5 puntos]. Sean los vectores

    u = (-1,2,3), v = (2,5,-2), x = (4,1,3), z = (4,1,-8)

    (1) [1 punto]. ¿Se puede expresar x como combinación lineal de u y v? Si es así, escribe dicha combinación lineal; si no es así, explica por qué.
    (2) [1 punto]. ¿Se puede expresar z como combinación lineal de u y v? Si es así, escribe dicha combinación lineal; si no es así, explica por qué.
    (3) [0'5 puntos]. ¿Son u, v y z linealmente independientes? Justifica la respuesta.

  18. [2'5 puntos]. Clasifica el siguiente sistema de ecuaciones según los valores del parámetro ,

  19. Considera la matriz

    (1) [1 punto]. Calcula AtA y AAt donde At denota la matriz traspuesta de A.
    (2) [1'5 puntos]. Siendo X una matriz columna, discute y, en su caso, resuelve la ecuación matricial

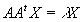
    según los valores del parámetro real .

  20. 3 puntos. Sea el sistema

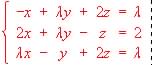
    a) (1 punto) Discutir la compatibilidad del sistema según los diversos valores de l
    b) (1 punto) Resolver el sistema para l = - 1
    c) (1 punto) Resolver el sistema para l = 2

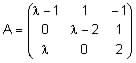
  21. a) (1 pu.to) Encontrar los valores de l para que la matriz


    es invertible.

    b) (1 punto) Para l = 2, hallar la inversa de A y comprobar el resultado.

    c) (1 punto) Resolver el sistema:


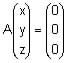
    para     l = 1

  22. Resolver el sistema formado por las tres ecuaciones:   x + y + z =3;    2x - y = 1;    - x + 2y + z = 2
    y justificar si tiene o no las mismas soluciones que el sistema     x + y + z = 3;    2x - y = 1.