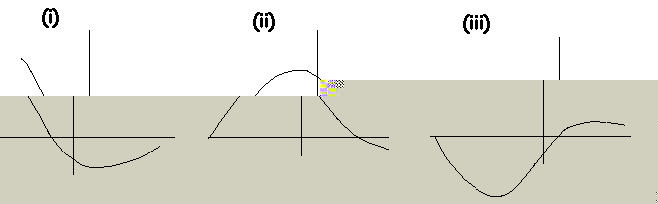
Las gráficas (i), (ii) y (iii) corresponden, no necesariamente por ese orden, a las de una función derivable f , su función derivada f ' y una primitiva F de f . identifica cada gráfica con su función justificando la respuesta.
definida por
donde t mide el tiempo en horas.(1) [1 PUNTO]. Calcula los intervalos en los cuales la capacidad de concentración aumenta y los intervalos en los que disminuye. ¿Cuándo es nula?
(2) [0'75 PUNTOS]. ¿Cuál es el mejor momento, en términos de su capacidad de concentración, para que la saltadora pueda batir su propia marca?
(3) [0'75 PUNTOS]. Representa graficamente la función de capacidad de concentración.
Una partícula se mueve a lo largo de la gráfica de la curva
.
En el punto P = (2 , -4/3) la abandona y sigue desplazándose a lo largo de la recta tangente a la curva.
(1) [1 PUNTO]. Halla la ecuación de dicha recta tangente.
(2) [0'5 PUNTOS]. Si el desplazamiento es de izquierda a derecha, encuentra el punto en el que la partícula encuentra al eje OX.
(3) [1 PUNTO]. Si el desplazamiento es de derecha a izquierda, encuentra el punto en el que la partícula encuentra a la asíntota vertical más próxima al punto P.
El alcalde de un pueblo quiere cercar un recinto rectangular cerrado para celebrar las fiestas. Para ello aprovecha una tapia existente como uno de los lados y dispone de 300 m. de tela metálica para hacer los otros tres.
(1) ¿Podrías indicar las dimensiones del recinto acotado de esa forma cuya área es la mayor posible?
(2) La comisión de fiestas del pueblo ha calculado que para montar las atracciones, pista de baile etc., necesitan 8.000 m2 . Teniendo en cuenta los cálculos realizados en el apartado anterior ¿será suficientemente grande el recinto que quiere preparar el alcalde?
Dada una circunferencia de radio r , se divide uno de sus diámetros en dos partes que se toman como diámetros de dos circunferencias tangentes interiores a la circunferencia dada. ¿Qué longitud debe tener cada uno de estos diámetros para que sea máxima el área de la región comprendida entre las circunferencias interiores y la exterior (la región rayada en la figura)?
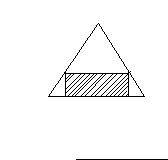
Dado un triángulo isósceles de base 8 cm. y altura 5 cm., calcula las dimensiones del rectángulo de área maxima que puede inscribirse dentro de dicho triángulo como se indica en la figura.
Desde la Tierra, que suponemos situada en el origen de coordenada del plano, se observa un objeto que sigue una trayectoria de ecuación
(donde la distancias se miden en años-luz) ¿Cuáles son las coordenadas del punto de la trayectoria cuya distancia a la Tierra es mínima y cuánto vale dicha distancia?
(1) Si el precio de un diamante es proporcional al cuadrado de su peso, demuestra que siempre se pierde valor al partirlo en dos trozos.
(2) Como puedes suponer, puede partirse en dos trozos con diferentes pesos de múltiples formas. Determina la partición que origina la máxima perdida de valor. Razona tu respuesta.
Sobre un terreno con forma de triángulo rectángulo cuyos catetos miden respectivamente, 100 y 200 metros, se quiere construir un edificio de planta rectangular como se muestra en la figura. Halla las dimensiones que debe tener dicha planta para que su superficie sea máxima.
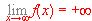. Haz un esbozo de la gráfica de f sin realizar ningún cálculo jjustificando cómo lo haces a partir de los datos.
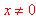por la relación
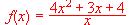
(1) Halla sus asíntotas.
(2) Determina sus extremos locales.
(3) Dibuja la gráfica de f indicando su posición respecto de las asíntotas.
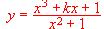
posee una asíntota que pasa por el punto (1 , 3).
Una cierta función p se define como el cociente de dos funciones derivables f y g, es decir, p(x)=f(x)/g(x). En un punto a de su dominio la función p tiene un mínimo relativo y sabemos que
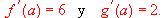¿Puedes obtener el valor de p(a)? Razona tu respuesta.
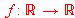que cumple las condiciones siguientes
,
>
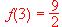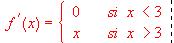
. (2) Razona si la función f es derivable en el punto x = 3. (3) Esboza la gráfica de esta función f.
la función definida por
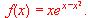
(1) Halla los máximos y mínimos relativos de esta función.
(2) Calcula
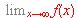
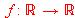definida por
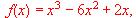halla la ecuación de la recta tangente a su gráfica en su punto de inflexión.
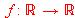sabiendo que es tres veces derivable, que
para cada punto x de
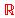y que
.
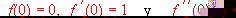definida por
Calcula, de manera razonada, su función derivada.
definida por
es derivable en todo su dominio.
(1) ¿Cuánto vale k? ¿Cuánto vale
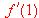? Justifica la respuestas.(2) Para el valor de k hallados en el apartado anterior, dibuja la región limitada por la gráfica de la función f , el eje OX , el eje OY y la recta x = 2.
(3) Halla el área de la región descrita en el apartado anterior.
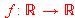la función definida por
.(1) Halla la ecuación de la recta tangente a la gráfica de la función f en su punto de inflexión.
(2) Dibuja el recinto limitado por la gráfica de la función f , la recta tangente en su punto de inflexión y el eje OY.
(3) Halla el área del recinto descrito en el apartado anterior.
se sabe que para cada x en dicho intervalo se tiene
De los números -3 , -2 , -1'25 , y 2'75 , ¿cuáles pueden ser el valor de la integral
?
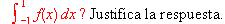definida por
, halla la que pasa por el origen de coordenadas.(2) Dibuja laregión limitada por la gráfica de
, la recta tangente hallada en el apartado anterior y el eje de ordenadas.(3) Halla el área de laregión descrita en el apartado anterior.
definida por
.(2) Dibuja la región limitada por la gráfica de f, el eje OX y la recta x = b donde b es la abcisa del punto de inflexión hallado en el apartado anterior.
(3) Calcula el área de laregión descrita en el apartado anterior.
por
.(2) Calcula el área de dicha región.
(2) Calcula
.
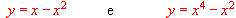(2) Halla el área del recinto descrito en el apartado anterior.
(2) Calcula el área de dicha región
(2) Estudia la derivabilidad de la función
definida por
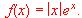
(3) Siendo f la función dada en el apartado anterior, calcula
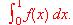
dada por
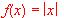.(1) Estudia la derivabilidad de f.
(2) Dibuja la gráfica de f.
(3) Halla
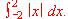
definida por
.(1) Determina los intervalos en los que la función f es creciente.
(2) Dibuja la región limitada por la gráfica de f, el eje de abcisas y las rectas de ecuaciones
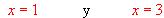
(3) Halla el área de la región descrita en el apartado anterior.
.(1) Calcula el espacio total que recorre la locomotora.
(2) Determina la velocidad máxima que alcanza la locomotora y el instante en que lo hace.
definida por
(1) Sea
la función definida por
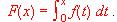¿Qué dice el teorema fundamental del cálculo integral sobre la función F ?(2) Halla
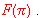
definida en la forma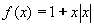 
(1) [1 punto]. Halla la derivada de f.
(2) [0'5 puntos]. Determina los intervalos de crecimiento y de decrecimiento de f.
(3) [1 punto]. Calcula
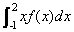
definida por f(x)=ax3+bx2+cx+d se sabe que tiene un máximo relativo en x=1, un punto de inflexión en (0,0) y que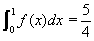 
. Calcula a, b, c y d.
y la recta de ecuación
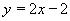.(2) [1'5 puntos]. Halla el área de la región descrita en el apartado anterior.
(donde Ln(x) es el logaritmo neperiano de x), determina cuál de las rectas tangentes a la gráfica de f tiene la máxima pendiente.
.
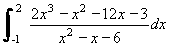
(1) [1'5 puntos]. Halla una recta que sea tangente a dicha curva y que forme un ángulo de 45º con el eje de abcisas.
(2) [1 punto] ¿Hay algún punto de la curva en el que la recta tangente sea horizontal? En caso afirmativo, halla la ecuación de dicha tangente; en caso negativo, explica por qué.
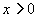por
(2) [1 punto]. Halla las regiones de crecimiento y de decrecimiento de f indicando sus máximos y mínimos locales y globales si los hay.
(3) [0'5 puntos]. Esboza la gráfica de f.
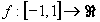
que cumple 
y
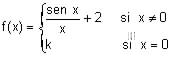
a) (1 punto) ¿Hay algún valor de k para el cual f(x) sea continua en x = 0?
b) (1 punto) ¿Hay algún valor de k para el cual f(x) sea derivable en x = 0?
c) (1 punto) Determinar sus asíntotas.
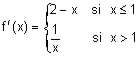
a) Hallar la expresión de f(x).
b) Obtener la ecuación de la recta tangente a f(x) en x = 2
La semicircunferencia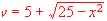 
· El eje OX
· El segmento que une los vértices (5, 0) y (5, 5).
· El segmento que une los vértices (-5, 0) y (-5, 5).
Halla el volumen de la figura obtenida al girar esa superficie una vuelta alrededor del eje OX