[2,5 PUNTOS]. Desde el origen de coordenadas pueden trazarse dos rectas tangentes a la circunferencia que tiene su centro en el punto (3, 0) y cuyo radio vale  . ¿Cuales son las ecuaciones de dichas rectas tangentes?
. ¿Cuales son las ecuaciones de dichas rectas tangentes?
Una circunferencia tiene por centro el punto C = (1 , 0) y su diámetro es 2. Halla la ecuación de la recta tangente a la circunferencia en el punto de abcisa x = 3/2 y ordenada positiva.
[2,5 PUNTOS]. Se tiene un paralelogramo uno de cuyos vértices es el punto (3 , 2) y dos de cuyos lados se encuentran contenidos, respectivamente, en las rectas r y s de ecuaciones 
Halla las ecuaciones de las rectas sobre las que se encuentran los otros dos lados.


(1) Encuentra el valor de a para que las rectas r y s son perependiculares. Para dicho valor, halla la ecuación de un plano que contenga a s y sea paralelo a r.
(2) Determina un valor positivo del parámetro a para el que la3 rectas r y s son coplanarias y halla la ecuación de la recta que es perpendicular a ambas y pasa por el punto P = (1, -2,3).
Determina la ecuación del plano que pasa por el punto P = (1 , 0 , 2), es paralelo a la recta  y es perpendicular al plano
y es perpendicular al plano  (1997)
(1997)
Halla la ecuación del plano que pasa por el punto A = (1 , 1 , 2) y es paralelo a las rectas r y s dadas por


Determina la ecuación de un plano que contenga a r y sea paralelo a s.
 .
.(2) Halla un punto A que está; sobre el eje OX y tal que el área del triángulo ABC valga 6. ¿Cuántas soluciones existen?
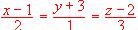
(2) Calcula elángulo que forman el plano calculado en el apartado anterior y la recta de ecuaciones 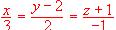 .
.
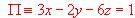 y sea la recta r dada en forma paramétrica por:
y sea la recta r dada en forma paramétrica por: 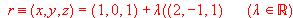 .
.(1) [0,5 Puntos] ¿Cómo se define la relación de paralelismo entre una recta y un plano?
(2) [0,75 Puntos]. En el caso concreto de la recta r y el plano
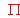 , ¿cómo averiguarías si son paralelos? Compru%ba si lo son.
, ¿cómo averiguarías si son paralelos? Compru%ba si lo son.(3) [0,5 Puntos]. ¿Cómo se define la relación de perpendicularidad entre una recta y un plano? (4) [0,75 Puntos]. En el caso concreto de la recta r y el plano
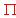 ¿cómo averiguarías si son perpendiculares? Comprueba si lo son.
¿cómo averiguarías si son perpendiculares? Comprueba si lo son.

(2) Si a = -1, ¿en qué punto se cortan?
Calcula de manera razonada, un plano que sea paralelo al plano de ecuación x + y + z = 1 y determine con los ejes coordenados un triángulo cuya área sea 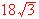 .
.
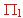 y
y 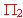 los planos de ecuaciones:
los planos de ecuaciones:  y
y 
Explica algún procedimiento para saber si un punto de
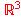 se encuentra entre
se encuentra entre 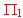 y
y 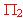 y aplícalo para saber si el punto P = (2, 2, 1) se encuentra o no entre dichos planos
y aplícalo para saber si el punto P = (2, 2, 1) se encuentra o no entre dichos planos
(1) [1 Punto]. Determina un punto Q del plano
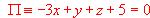 de forma que el vector PQ sea perpendicular al plano
de forma que el vector PQ sea perpendicular al plano 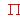 .
.(2) [1 Punto]. Determina un punto M de la recta
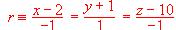 de forma que el vector MP sea paralelo al plano
de forma que el vector MP sea paralelo al plano 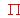 .
.(3) [0,5 Puntos]. Calcula el área del triángulo MPQ.
(2) Halla el punto simétrico de P = (1, 2, 3) repecto de la recta r dada por 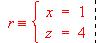
(3) Halla el punto simétrico de P = (1, 2, 3) respecto del punto Q = (1, 2, 4).
(1) Halla la ecuación del lugar geométrico de los puntos que se encuentran a igual distancia del punto P que del Q .
(2) Halla la ecuación del plano que corta perpendicularmente y en su punto medio al segmento que une los puntos P y Q.
 corta a los ejes coordenados.
corta a los ejes coordenados.(1) Describe un procedimiento para hallar el volumen de tetraedro y calcula efectivamente su valor.
(2) Calcula razonadamente las coordenadas del punto simétrico al origen de coordenadas respecto al plano
 .
.
A = (1, 2, 3), B = (0, 1, -2) C = (3, 1, 0) y D = (mm, -1, 4).
(1) ¿Existe algún valor de m para el que los cuatro puntos están sobre una misma línea recta? En caso afirmativo, determina dicha recta; en caso negativo, di porque no están alineados.
(2) ¿Existe algún valor de m para el que los cuatro puntos están sobre un plano? En caso afirmativo, determina dicho plano; en caso negativo, di por qué no son coplanarios.
(3) Para m = 2, ¿determinan estos cuatro puntos un tetraedro? En caso afirmativo, calcula el volumen de dicho tetraedro, en caso negativo, di por qué no lo determinan.
(1) Halla la recta r que pasa por D y es perpendicular al plano determinado por los puntos A, B y C.
(2) Halla la mínima distancia entre la recta r y la recta que pasa por los puntos A y B.
(3) Calcula el volumen del teraedro.
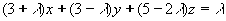
(con 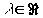 ) contienen una misma recta y
halla unas ecuaciones paramétricas de dicha recta.
) contienen una misma recta y
halla unas ecuaciones paramétricas de dicha recta.
 .
. (2) [0'75 puntos]. Determina si el punto X=(3,3) es interior, es exterior o está en la circunferencia.
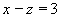 que está más cerca del punto
P=(3,1,4) así como la distancia entre el punto P y el plano dado.
que está más cerca del punto
P=(3,1,4) así como la distancia entre el punto P y el plano dado.
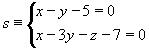
que equidiste de los puntos P=(1,0,-1) y Q=(2,1,1).
(2) [0'5 puntos]. Calcula el área del triángulo determinado por los puntos P, Q y R.
b) (1 punto) Comprobar que el anterior lugar geométrico es una cónica. Indicar el tipo de cónica que es y hallar sus focos.
b) (1 punto) Hallar el área del triángulo cuyos vértices son los puntos P, Q y R.
c) (1 punto) Encontrar todos los puntos S del plano determinado por P, Q y R de manera que el cuadrilátero de vértices P, Q, R y S sea un paralelogramo.