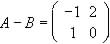Se quieren obtener 10 kg. de pasta de trigo, arroz y maíz, cuyos precios son 20, 40 y 25 ptas/kg. respectivamente. hallar la cantidad de cada materia que ha de formar la pasta, sabiendo que el precio resultante ha de ser de 40 ptas/kg. y que la cantidad de arroz ha de ser doble que la de maíz.
? .
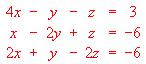
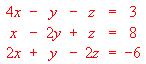
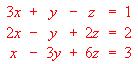
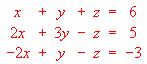
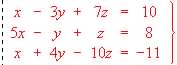
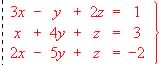
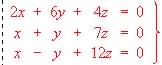
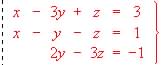
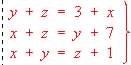
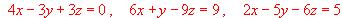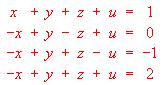
Discutir, según los valores del parámetro , el sistema de ecuaciones lineales
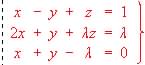
Un capitán tiene tres compañías: una de suizos, otra de zuavos y una tercera de sajones. Al asaltar una fortaleza promete una recompensa de 901 escudos
que se repartirán de la siguiente forma: el soldado que primero suba y todos
los de su compañía recibirán un escudo; el resto de la recompensa se repartirá
a partes iguales entre el resto de los soldados.
Sabiendo que si el primero que sube es un suizo, los de las demás compañías
reciben medio escudo; si el primero es zuavo, los restantes reciben un tercio
de escudo, y si el primero es sajón, un cuarto de escudo, ¿cuántos hombres hay
en cada compañía?
Una empresa cinematográfica dispone de tres cines C1 , C2 , y C3. Cierto día, en cada uno de ellos, proyecta tres películas, P1 , P2 y P3, (P1 en sesión de mañana, P2 en sesión de tarde, y P3 en sesión de noche). El nº de asistentes, (expresado en centenares), a cada una de ellas se indica en la siguiente tabla:
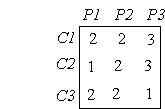
Sabiendo que los ingresos obtenidos en ese día , en C1 , C2 y C3, fueron de 150000, 140000 y 90000 ptas.., respectivamente. Calcular el precio de la entrada para cada una de las tres películas.
Con 450 gramos de medicamento se fabricaron 60 pastillas de tres tipos: grandes, medianas y pequeñas. Las pastillas grandes pesan 20 gramos, las medianas 10 gramos y las pequeñas 5 gramos. Si el total de pastillas grandes y medianas es la mitad del número de pastillas pequeñas, ¿cuántas se fabricaron de cada tipo?
Una marca comercial utiliza tres ingredientes (A, B, y C) en la elaboración de tres tipos de pizzas (P1, P2 y P3). P1 se elabora con 1 unidad de A, 2 de B y 2 de C: P2 con 2 unidades de A, 1 de B y 1 de C, y P3 con 2 unidades de A, 1 de B y 2 de C. El precio de venta es de 1.200 ptas.. para P1, 1.025 ptas.. para P2 y 1225 ptas. para P3. Sabiendo que el margen comercial (beneficio) es de 400 ptas.. en cada una de ellas, ¿qué le cuesta a dicha marca comercial cada unidad de A, B y C? Justificar la respuesta.
En la tabla siguiente se indica la audiencia prevista (en miles de personas) por tres cadenas de televisión (a, B y C) en determinada semana, y en cada uno de los tres segmentos horarios (Mañana, Tarde y Noche)
| A | B | C | |
| Mañana | 40 | 60 | 150 |
| Tarde | 60 | 50 | 20 |
| Noche | 150 | 90 | 70 |
Sin embargo, como consecuencia de la calidad de los programas emitidos, se ha producido en la audiencia prevista (en todos los segmentos horarios) una reducción de un 10% para la cadena A, una reducción de un 5% para la cadena B y un aumento de un 20% para la cadena C. a) Obtener la matriz que expresa la audiencia real obtenida por dichas cadenas de televisión. b) Sabiendo que el beneficio por espectador es de 500 ptas. por la mañana, 700 ptas. por la tarde y 1.000 ptas. por la noche, obtener los beneficios obtenidos por cada una de las tres cadenas.
Una lechería vende leche entera, semidesnatada y desnatada a 100, 120 y 150 ptas el litro, respectivamente. Cierto día vendió 50 litros más de leche entera que de desnatada, y si hubiese vendido 5 litros más de leche desnatada, entonces el número de litros vendidos de leche desnatada sería cuatro veces el de leche semidesnatada vendida. Sabiendo que los ingresos totales obtenidos en dicho día fueron de 26.150 ptas, ¿cuántos litros de cada tipo de leche vendió? b) ¿Cuál sería ese beneficio máximo?
Una marca comercial dispone de tres establecimientos (E1, E2 y E3) en los que prepara cuatro platos combinados (P1, P2, P3 y P4) que vende al precio de 400, 500, 500 y 600 pesetas, respectivamente. Cierto día el número de platos combinados servidos (en cada uno de los establecimientos) es el indicado en la matriz siguiente:
| P1 | P2 | P3 | P4 | |
| E1 | C | 3 | 4 | B |
| E2 | A | B | 5 | 5 |
| E3 | 10 | A | B | 5 |
Determinar los valores de A, B y C, sabiendo que los ingresos obtenidos dicho día en E1, E2 y E3, fueron de 7.400, 8.700 y 10.500 pesetas, respectivamente. Justificar la respuesta.
En una tienda, un cliente se ha gastado 15000 ptas en la compra de 12 artículos entre discos, libros y carpetas. Cada disco le ha costado 2000 ptas,cada libro 1500 ptas y cada carpeta 500 ptas. Se sabe que entre discos y carpetas hay el triple que de libros.
(1.5 puntos) Formule el sistema de ecuaciones asociado al enunciado anterior.
(1.5 puntos) Determine cuántos artículos ha comprado de cada tipo.
"Un comerciante ha vendido 600 camisetas por un total de 638000 ptas. Su precio original era de 1200 ptas por camiseta, pero ha vendido en las rebajas una parte de ellas con un descuento del 30% del precio original y otra parte con un descuento del 40%. Sabiendo que el número total de camisetas rebajadas fue la mitad del número de las que vendió a 1200 ptas, calcular cuántas camisetas se vendieron a cada precio."
(2 puntos) Resuleva el sistema formado por las ecuaciones:
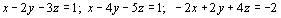
Una autoescuela tiene abiertas tres sucursales en la ciudad. El número total de matriculados es 352, pero los matriculados en la tercera son tan sólo una cuarta parte de los matriculados en la primera. Además, la diferencia entre los matriculados en la primera y los matriculados en la segunda es inferior en dos unidades al doble de los matriculados en la tercera.
a) Plantear un sistema de ecuaciones para averiguar el número de alumnos matriculados en cada sucursal.
b) Resolverlo.
a) Tres amigos, Marcos, Luis y Miguel, son aficionados a la música. Entre los tres poseen un total de discos compactos (CD), comprendidos entre 16 y 22.
Marcos presta 4 CD a Miguel, Luis presta 1 CD a Marcos y Miguel presta 2 CD a Luis, con lo cual los tres amigos tiene ahora el mismo número de CD.
¿Cuántos CD pueden tener en total .
b) Si A y B son dos matrices cualquiera, ¿es correcta la siguiente cadena de igualdades?:
(A + B)(A - B) = A(A - B) + B(A - B) = AA - AB + BA - BB = A 2 - AB + BA - B 2 = A 2 - B 2
Justifique la respuesta.
Los gastos diarios de tres estudiantes, Marta, Raúl y Pedro suman 1545 pesetas. Si a los que gasta Marta se le suma el triple de la diferencia entre los gastos de Raúl y Pedro obtendremos lo que gasta Pedro. Ocho veces la diferencia entre el gasto de Raúl y el de Marta es igual al gasto de Marta.
Averiguar cuál es la cantidad que gasta cada uno.
Se mezclan tres clases de vino de la siguiente manera:
e) 5 litros de Tenerife, 6 de La Palma y 3 de Lanzarote, resultando una mezcla de
120 pesetas/litro.
f) 1 litros de Tenerife, 3 de La Palma y 6 de Lanzarote, dando un vino de 111
pesetas/litro.
g) 3 litros de Tenerife, 6 de La Palma y 6 de Lanzarote, dando un vino de 116
pesetas/litro.
Halla el precio por litro de cada clase de vino.
Escribe el sistema en forma matricial y resuélvelo:
Estudiar el sistema que se expresa a continuación, de dos ecuaciones con dos incógnitas x e y, en función del parámetro n.
-4n 3 x - y = 8n 2 - 20n + 4
Si se mezclan 60 litros de vino blanco con 20 litros de vino tinto, se obtiene un vino de 10 grados (10% de alcohol). Si, por el contrario, se mezclan 20 litros de blanco con 60 litros de tinto, se obtiene un vino de 11 grados. ¿Qué graduación tendrá una mezcla de 40 litros de vino blanco con 40 litros de vino tinto?
Un país importa 21.000 vehículos mensuales de las marcas X, Y, Z al precio de 1,2, 1,5 y 2 millones de pesetas, respectivamente. Si el total de la importación asciende a 32.200 millones, y de la marca X se importa el 40% de la suma de las otras dos marcas, ¿cuántos vehículos de cada marca entran en ese país?
Tres familias van a una heladería. La primera familia pide dos helados grandes, uno mediano y uno pequeño; la segunda familia pide uno grande, dos
medianos y dos pequeños, y la tercera familia pide dos grandes y tres pequeños.
a) Escribe una matriz 3x3 que exprese el nombre de los helados grandes, medianos y pequeños que pide cada familia.
b) Si la primera, la segunda y la tercera familia han gastado en total en la heladería 700, 800 y 775 pesetas, respectivamente, calcula el precio de un helado grande, el de un helado mediano y el de un helado pequeño.
De tres amigos, Antonio, Juan y Pedro, se sabe lo siguiente:
"El doble de la edad de Antonio más el triple de la edad de Juan es tres años superior a cuatro veces la edad de Pedro. El triple de la edad de Pedro menos el doble de la edad de Juan es siete años inferior al doble de la edad de Antonio. El doble de la edad de Antonio más el doble de la edad de Pedro es tres años inferior a cinco veces la edad de Juan".
Calcular la edad de cada uno de los tres amigos.
a) Propón un ejemplo de un sistema de tres ecuaciones con tres incógnitas que sea compatible y determinado.
b) La suma de las cifras de un número comprendido entre 100 y 999 es 13. Si intercambiamos las cifras de las unidades y la de las centenas, el número disminuye en 198. Si intercambiamos las de las unidades y las de las decenas, el número aumenta en 36. ¿Cuál es el número?
a) Dado el sistema de ecuaciones lineales 
,
expresarlo en la forma matricial AX = B, calcular la matriz inversa de A y resolverlo.
Un tanque de un camión de 10.000 litros de volumen se llenó con agua procedente de dos depósitos de almacenamiento, A y B. El agua del depósito A se bombeó a dicho tanque a razón de 20 litros por minuto. El agua del depósito B se bombeó a dicho tanque a razón de 30 litros por minuto. Ambas bombas operaron el mismo tiempo; sin embargo, a causa de un fusible fundido, la bomba A estuvo parada 10 minutos. ¿Cuántos litros de cada depósito de almacenamiento se utilizaron para llenar el tanque del camión?
Los estudiantes de cierto curso venden camisetas, gorras y banderines para ayudarse a pagar un viaje. Cada camiseta la venden a 800 PTA, cada gorra a 120 PTA y cada banderín a 200 PTA. Los costes de cada prenda son de 300 PTA por camiseta, 20 PTA por gorra y 80 PTA por banderín. El beneficio neto obtenido es de 67.400 PTA y el gasto total es de 34.600 PTA. Sabiendo que se han vendido un total de 270 unidades en conjunto, calcula cuántas se han vendido de cada clase.
En un centro se imparten los cursos 1º, 2º y 3º de ciertas enseñanzas. Los profesores tienen asignado un número de horas de clase, tutorías y guardias a cubrir de acuerdo con la siguiente matriz:
El centro paga cada hora de clase a 2.000 PTA, cada hora de guardia a 500 PTA y cada hora de tutoría a 1.000 PTA, según el vector:
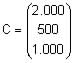
El centro dispone de 5 profesores para primer curso, 4 para segundo y 6 para tercero, representados por el vector:
P = (5 4 6)
Calcula cada uno de los siguientes productos de matrices e interpreta los resultados.
a) PM b) MC c) PMC
Sea la matriz
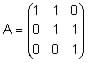
a) Calcula una matriz B tal que se cumpla A + B = AAT
b) Para la matriz B anterior, obtén la expresión de Bk
Resolver la ecuación matricial AX = BX + C, siendo:
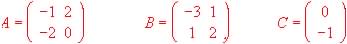
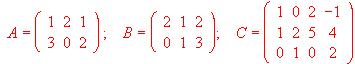
Calcular (A + B) · C
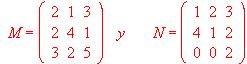
Hallar M · N 
N · M
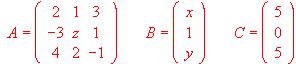
Calcular x, y, z, sabiendo que A · B = C
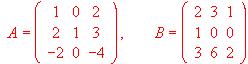
Calcular AxB - BxC.
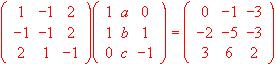
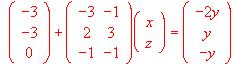
a) Considerar una matriz A de orden m x n con 
Razonar si se puede calcular la expresión AAt - At A, siendo At la matriz traspuesta de A.
b) Considerar la matriz 
Resolver por el método de Gauss:
i) El sistema de ecuaciones lineales homogéneo cuya matriz de coeficientes es At A.
ii) El sistema de ecuaciones lineales homogéneo cuya matriz de coeficientes es AAt
Una fábrica decide distribuir sus excedentes en tres productos alimenticios A, B y C a cuatro países de África P1, P2, P3 y P4 según se describe en la matriz M1 (cantidades en toneladas). Esta fábrica ha recibido presupuesto de dos empresas para el transporte de los productos a los países de destino como indica la matriz M2 (en euros por tonelada).
Efectúa el producto de las matrices y responde a las cuestiones:
i) ¿Qué representa el elemento a11 de la matriz producto?
ii) ¿Qué elemento de la matriz producto nos indica lo que cuesta transportar el producto C con la empresa E2?
iii) Indica qué elementos de la matriz producto te permiten decir cuál es la empresa que más barato transporta el producto B a todos los países.
Sea el sistema:
.
a) (0.5 puntos) Expréselo en forma matricial.
b) (0.5 puntos) ¿La matriz de los coeficientes posee inversa? Justifique la respuesta.
c) (2 puntos) Resuélvalo y clasifíquelo en cuanto al número de soluciones
a) (2 puntos) Determine dos números sabiendo que al dividir el mayor por el menor obtenemos 7 de cociente y 2 de resto, y que la diferencia entre el triple del mayor y el menor es 106.
b) (1 punto) Resuelva el siguiente sistema e interprete gráficamente sus soluciones:
a) (1 punto) Un establecimiento pone a la venta tres tipos de camisas A, B y C. Se sabe que la razón entre los precios de las camisas C y B es 19/18 y entre los de B y A es 6/5. Al comprar tres camisas, una de cada clase, se pagan 13000 pts. Plantee el sistema de ecuaciones que permita conocer el precio de cada camisa.
b) (2 puntos) Siendo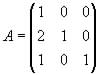 
y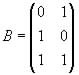 
, razone si posee solución la ecuación matricial A · X = B y, en caso afirmativo, resuélvala.
(3 puntos) Resuelva la siguiente ecuación matricial: 
,
siendo
, 
, 
.
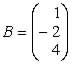a) (1 punto) Determine los valores de x e y que hacen cierta la siguiente igualdad:
.
b) (2 puntos) Determine la matriz X de dimensión 2x2 tal que:
.
Se considera la matriz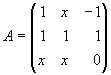 
.
a) (1.5 puntos) Calcule los valores de x para los que no existe la inversa de A
b) (1.5 puntos) Para , x = 3 calcule, si es posible, 
.
Determinante de una matriz cuadrada. Propiedades.
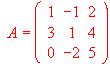; Hallar | A | y | A | t .
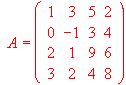en otro más sencillo de igual valor.
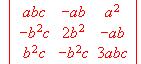
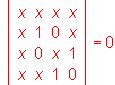
, se llaman "valores propios" de dicha matriz a los valores de l , tales que el determinante de la matriz A - lI sea nulo. Hallar los valores propios de A.
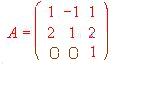
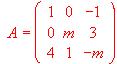, Averiguar para que valores de m existe A-1 . Calcular A-1 para m = 2.
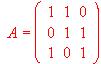, Estudiar si tiene inversa y en caso afirmativo calcularla.
siendo,
y 
Encuentra las matrices A y B de dimensiones 2 x 2 que cumplen:
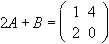y 