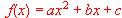, pase por los puntos (0, 1) y (1, 3), y la función f tenga un máximo en el punto x = 1.Represéntese gráficamente la función.
, pase por los puntos (0, 1) y (1, h), y la función f tenga un mínimo en el punto x = 1, ¿Cómo debe ser h para que exista solución?
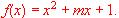
Determínese, si es posible, el valor de m en cada uno de los casos siguientes:
(a) Que f (-2) =8
(b) Que la gráfica de f contenga el punto (3, 3).
(c) Que la gráfica de f pase por el origen.
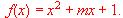
Determínese, si es posible, el valor de m en cada uno de los casos siguientes:
(a) Que la gráfica de f sea tangente al eje OX.
(b) Que el eje de simetría de la gráfica sea la recta x = 4.
(c) Que la función alcance su valor mínimo en x = -1.
(d) Que se verifique la relación
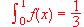.(e) Que la función tenga algún máximo.
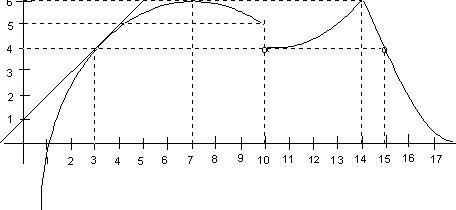
a) (0.75 puntos) Obtener los intervalos de crecimiento y de decrecimiento.
b) (0.75 puntos) Obtener los puntos del dominio donde sea discontinua.
c) (0.75 puntos) Obtener los valores de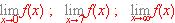 
d) (0.75 puntos) Obtener los valores de f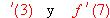 
a) (05 puntos) Hallar los intervalos de crecimiento y decrecimiento.
b) (0,5 puntos) Determinar los intervalos de concavidad y convexidad.
c) (1 punto) Hallar los puntos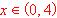 
tales que f(x) = 0 y determinar, en ese intervalo, dónde se alcanzan los máximos locales.
d) (1 punto) Determinar las asíntotas verticales y razonar si existen asíntotas horizontales.
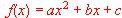, se sabe que la gráfica de su derivada f ' es la recta que pasa por los puntos (2, -1) y (-2, 1). También se sabe que el máximo de f es 1. Determine a, b y c.
a) Determinar el que tiene unas diagonales tales que su suma de cuadrados sea lo más pequeña posible.
b) Determinar el que tiene las diagonales de la menor longitud posible.
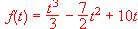
Se pide:
a) Sabiendo que en uno de los 5 primeros años de producción alcanza un máximo, hallar dicho máximo y el valor de la cantidad de madera producida.
b) Sabiendo que antes de los 20 primeros años la producción alcanza un mínimo, hallar dicho máximo y el valor de la producción en dicho año.
c) Esbozar la gráfica de la función f .
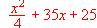,si toda la producción diaria se vende completamente a un precio unitario, en pta., de
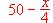
halle el número de unidades diarias que deben fabricarse para alcanzar un beneficio máximo.
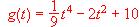. Se pide:
a) Probar que el coeficiente de elasticidad es siempre (para cualquier valor de t) positivo.
b) Hallar el valor de la temperatura para la que la elasticidad es mínima. Hallar el valor del mínimo de la elasticidad.
a) (2 puntos) ¿Cuál es la longitud de lado de los cuadrados que deben suprimirse para que resulte una caja de volumen máximo?
b) (1 punto) ¿Cuánto vale dicho volumen?
Calcule:
a) (2 puntos) Las dimensiones de la ventana para que el coste del marco sea mínimo.
b) (1 punto) El coste del marco.
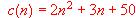
Se sabe que el número de unidades fabricadas diariamente desde el inicio de la jornada laboral hasta la hora t es
a) (1 punto) Exprese analíticamente el coste de fabricación en función de t .
b) (1 punto)Calcule el costo de fabricación al cabo de una jornada de trabajo de 7 horas.
c) (1 punto) En el caso de que se fabricaran 50 unidades y de que se vendiese cada unidad a 200.000 Pta., calcule el beneficio obtenido.
a) (1 punto)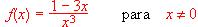
b) (1 punto) 
(ln : logaritmo neperiano)
c) (1 punto)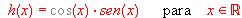 
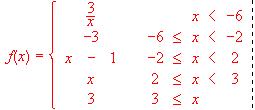
a) (1,5 puntos) Represente la función.
b) (1,5 puntos) Determine los puntos en los que la función no es derivable.
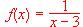definida para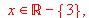 
a) (1 punto) Estudie su comportamiento para valores grandes de "x" y alrededor de x = 3.
b) (1 punto) Estudie su crecimiento y decrecimiento.
c) (1 punto) Represente su gráfica.
a) (2 puntos) Determine la longitud del lado del cuadrado que se tiene que suprimir para que el depósito resultante tenga la mayor capacidad posible.
b) (1 punto) Determine también la capacidad máxima.
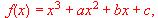
verifica que su gráfica pasa por el punto (-1, 0) y tiene tangente paralela al eje OX en el punto (0, 4).
a) (1 punto) Determine la función f (calcule a, b y c).
b) (1 punto) Calcule la recta tangente a la gráfica de f en el punto de abcisa 3.
c) (1 punto) Calcule el punto de inflexión de f .
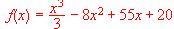
donde x representa el número de unidades vendidas en un día.
a) (1 punto) Esboce la gráfica de la función f .
b) (1 punto) ¿Qué número de unidades vendidas por día proporciona el mayor beneficio, teniendo en cuenta que la empresa no produce más de 12 ordenadores por día?
c) (1 punto) ¿Qué número de unidades vendidas por día proporciona el menor beneficio teniendo en cuenta que la empresa produce más de 6 y no más de 12 ordenadores por día?
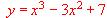, estudiando con detalle crecimiento y decrecimiento, máximos y mínimos, y concavidad y convexidad.
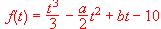
Se sabe que a la temperatura de 6º C el índice alcanza un máximo local y que a la temperatura de 12 º C el índice alcanza un mínimo local.
a) (1 punto) Halle a y b .
b) (1 punto) Sabiendo que el bacilo sólo puede vivir entre 4º C y 16º C halle la temperatura para la que el índice de crecimiento es máximo.
c) (1 punto) Esboce la gráfica de la función f considerada definida sobre 
.
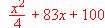
Si diariamente se vende toda la producción de vidrio reciclado al precio de
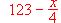
miles de pesetas por tonelada, halle la cantidad de vidrio que debe reciclarse cada día para lograr un beneficio máximo.
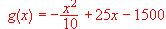
a) (2 puntos) Represente gráficamente la funcióng (x).
b) (0,5 puntos) ¿Cuál es el precio con el que se alcanza el máximo de ganancia?
c) (0,5 puntos) ¿Cuál es la ganancia máxima diaria que puede obtenerse.
De dos funciones f y g, se sabe que la representación gráfica de sus funciones derivadas es una recta que pasa por los puntos (0,2) y
(2,0) (para la derivada de f) y una parábola que corta al eje OX en (0,0) y (4,0) y tiene por vértice (2,1) (para la derivada de g). Utilizando las gráficas de tales derivadas:
(2 puntos) Estudie el crecimiento y decrecimiento de f y g.
(1 punto) Determine, si existen, máximos y mínimos de f y g.
Sea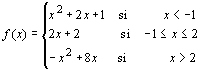 
(1 punto) Estudie su continuidad y derivabilidad.
(2 puntos) Represente gráficamente la función y, a la vista de su gráfica, determine sus máximos y mínimos relativos, así como el crecimiento y decrecimiento.
Calcule las funciones derivadas de las siguientes funciones, simplificando su expresión cuando sea posible:
(1 punto)
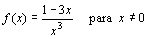
(1 punto)
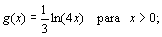(ln: logaritmo neperiano)
(1 punto) h(x)=cos(x).sen(x) para
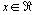
Los dueños de un manantial de agua mineral calculan que, si venden cada botella de agua a un precio de x ptas, tendrán una ganacia diaria (en miles de pesetas):
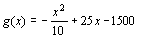
(2 puntos) Represente gráficamente la función g(x).
(0.5 puntos) ¿Cuál es el precio con el que se alcanza el máximo de ganancia?
(0.5 puntos) ¿Cuál es la ganancia máxima diaria que puede obtenerse?
Cierta empresa de material fotográfico oferta una máquina que es capaz de revelar y pasar a papel 15,5 fotografías por minuto. Sin embargo, sus cualidades se van deteriorando con el tiempo, de forma que el número de fotografías por minuto será función de la antigüedad de la máquina, de acuerdo a la siguiente expresión (F(x) representa el número de fotografías por minuto cuando la máquina tiene x años):
a) Estudiar la continuidad de la función F.
b) Comprobar que el número de fotografías por minuto decrece con la antigüedad de la máquina. Justificar que si tiene más de 5 años revelará menos de 10 fotografías por minuto.
c) Justificar que, por muy vieja que sea la máquina, no revelará menos de 5 fotografías por minuto.
Dada la función 
donde a es una constante,
a) Encontrar una primitiva de f.
b) Si F es una primitiva de f, ¿puede serlo también G(x) = F(x) + 2x?
c) Encontrar a sabiendo que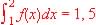 
Dada la función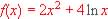 
, se pide:
a) Cuál es el dominio de definición de f(x)?
b) Determinar los intervalos de crecimiento y decrecimiento de f(x). razonar si existen máximo y mínimo y, en caso afirmativo, calcularlos.
c) Determinar los intervalos de concavidad y convexidad de f(x). Razonar si existen puntos de inflexión y, en caso afirmativo, calcularlos.
d) Determinar, si existen, las asíntotas de f(x).
Un rectángulo mide 8 dm de largo y 4 dm de ancho. De cada esquina se recorta un cuadrado de lado x con el fin de hacer una caja sin tapa.
b) Calcule el volumen de la caja en función de x.
c) Halle x para que el volumen sea máximo.
d) Halle dicho volumen máximo.
a) Calcula la derivada de cada una de las siguientes funciones:
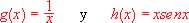
b) Estudia el crecimiento y decrecimiento de una función cuya función derivada viene dada gráficamente por la recta que pasa por los puntos (-1, 0) y (0, 1).
Dada la función 
se pide:
i) Gráfica de la misma.
ii) Estudiar su continuidad y hallar a para que sea continua en x = 4.
iii) Determinar intervalos de crecimiento y decrecimiento.
iv) Hallar la pendiente de la recta tangente a f(x) en x=3 y x=5.
Un publicista diseña un panel publicitario que tiene la siguiente forma: base horizontal de 10 metros de longitud y resto del contorno limitado por la función
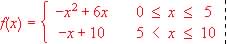
Se pide:
i) Dibujar la gráfica del recinto correspondiente al cartel publicitario.
ii) Calcular la superficie del mismo
El dueño de un manantial de agua llega a la conclusión de que, si el precio a que vende la botella es x pesetas, sus beneficios vendrán dados por la fórmula
Representa la función precio-beneficios e indica cuál será el precio de la botella para obtener el beneficio máximo.
Sea la función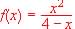 
.
1. Su dominio de definición.
2. Sus asíntotas.
3. Situación de la curva en relación a sus asíntotas.
4. Máximos y mínimos.
5. Intervalos de crecimiento y decrecimiento.
6. Área encerrada por la curva, la asíntota correspondiente y las rectas x = k,
x = 2k, siendo k el punto en el que la función tiene un máximo relativo.
Deseamos comprar 18 ordenadores y en el mercado hay dos tipos. Sabemos que el beneficio que podemos obtener de su uso está dado por: El producto del número de ordenadores de un tipo que se compra por el cuadrado del número de
ordenadores del otro tipo que se adquiere.
Determinar el número de ordenadores de cada tipo que debemos adquirir para
que el beneficio sea máximo.
Se ha lanzado verticalmente hacia arriba una piedra. La altura en metros alcanzada al cabo de t segundos viene dada por la expresión e=f(t)=20t-2t 2 .
a) Halla la velocidad media en el intervalo de tiempo comprendido entre t=0 y t=5
segundos.
b) ¿En algún momento la velocidad
Calcular el área del recinto limitado por la curva y = 2x 3 - 2x y el eje de abscisas.
Se desea construir una caja abierta (sin tapa) recortando cuadrados iguales de cada una de las esquinas de una hoja de cartón rectangular de dimensiones 3 y 8 dm. Calcular la longitud del lado del cuadrado que se ha de cortar para obtener un caja de volumen máximo.
Considera la función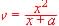 
Di para qué valores del parámetro a la función es creciente en el punto de abscisa x = 1.
Una compañía de transportes ha comprobado que el número de viajeros diarios depende del precio del billete, según la función:
n(p) = 3000 - 6p
donde n(p) es el número de viajeros cuando p es el precio del billete.
Obtener:
a) La función que expresa los ingresos diarios (I) de esta empresa en función del precio del billete (p).
b) El precio del billete que hace máximos dichos ingresos.
c) ¿A cuánto ascenderán dichos ingresos máximos?
Justificar las respuestas.
Dada la función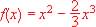 
, calcular:
a) los puntos de corte con los ejes.
b) intervalos de crecimiento y decrecimiento.
c) intervalos de concavidad y convexidad.
d) asíntotas.
e) Representar gráficamente f(x).
En su modelo para los costes de almacenamiento y transporte de materiales para el proceso de manufactura, Lancaster (1976) obtiene la siguiente función de coste:
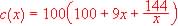
donde C(x) es el coste total (en dólares) de almacenamiento y transporte (durante tres meses) de x toneladas de material.
a) ¿Qué cantidad de materiales hace que el coste sea mínimo?
b) ¿Cuáles son las asíntotas de esta función?
c) Representar dicha función para los valores de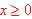 
.
a) Calcula p y q de modo que la curva y = x2 + px + q contenga al punto (– 2, 1) y presente un mínimo en x = – 3.
b) Halla el área del recinto acotado delimitado por la curva y = x2 + 4x + 5 y la recta y = 5.
El número de individuos, en millones, de una población viene dado por la función:
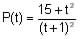
a) La población inicial.
b) El año en el que se alcanzará la mínima población. ¿Cuál será el tamaño de ésta?
c) ¿Cuál será el tamaño de la población a largo plazo?
Un club deportivo cuenta con un número de socios que viene dado (en miles de personas) por la función
donde x indica el número de años desde la última remodelación.
a) Halla el año en el que el club ha tenido el mayor número de socios.
b) El cuarto año se remodeló de nuevo. Indica razonadamente si esta remodelación tuvo éxito o no.
Sea la función
a) Halla los valores de a y b de forma que f tenga un máximo en x = 1 y un mínimo en x = 2
b) Halla el área de la región limitada por la gráfica f(x) y el eje OX entre x = 0 y x = 3
Los beneficios que se obtienen de la venta de x unidades de un determinado producto viene dado por la expresión:
B(x) = – 2x3 + 216x – 256
a) Determina el número de unidades a vender para el que se maximiza el beneficio medio, B(x)/x.
b) ¿Para qué número de unidades se obtiene el máximo beneficio?
Halla las rectas tangentes a la curva:
Que sean paralelas a la recta y = 9x + 4
Dada la curva de la función:
calcúlense las rectas tangentes a la misma, que sean paralelas a la recta de la ecuación y = - x
Se considera la función:
a) Hállense sus máximos y mínimos.
b) Determínense sus intervalos de crecimiento y decrecimiento.
c) Represéntese gráficamente.
Representar gráficamente la función:
¿En qué puntos es continua la función?
¿Cuál es la gráfica de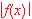 
Representar gráficamente la curva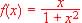 
encontrando:
a) Dominio, corte con los ejes y simetrías.
b) Asíntotas y regiones.
¿Cuántos extremos tendrá, al menos, la curva y de qué tipo? Hallarlos.
Encontrar entre todos los rectángulos de perímetro 2p el que tiene diagonal mínima.
De una función f(x) se sabe que está definida en el intervalo [0, 4] y que la gráfica de su derivada f'(x) es la línea quebrada que une los puntos (0, 1), (2, -1) y
(4, 1).
Hallar razonadamente los intervalos de crecimiento y decrecimiento de f(x) y sus
extremos relativos.
El consumo de combustible (en centenares de litros) de cierta aeronave durante un total de 5 horas de vuelo, viene dado por la función:
a) Representa dicha función.
b) Interpreta la gráfica obtenida.
a) Dada la función
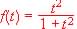
estudiar: cortes con los ejes, crecimiento y decrecimiento, asíntotas.
b) Si y = f(t), t ³ 0 nos da la relación entre los beneficios (en millones de pesetas), obtenidos por la venta de un producto y el tiempo t (en años) que éste lleva en el mercado, ¿durante cuánto tiempo no se superó el medio millón de pesetas de beneficios?.
Supóngase que durante los últimos 4 años las ventas en miles de unidades de los productos A y B vienen dadas por
a) ¿En qué períodos se vendió mas cantidad de producto A que del B?.
b) Período de tiempo durante el que las ventas de B superaron las 3 mil unidades.
Dada la función a) (1 punto) Calcule el valor de "
Las ganancias de una empresa, en millones de pesetas, se ajustan a la función
Sea la función a) (1 punto) Represéntela gráficamente.
El estudio de la rentabilidad de una empresa revela que una inversión de x millones de pesetas produce una ganancia de f(x) millones de pts, siendo:
Un objeto se lanza verticalmente hacia arriba de modo que la altura "h" (en metros) a la que se encuentra en cada instante "t" (en segundos) viene dada por la expresión:
(3 puntos) Determine los valores que han de tomar "a" y "b" para que la función:
sea derivable.
La gráfica de la función derivada de una función
El consumo de luz (en miles de pesetas) de una vivienda, en función del tiempo transcurrido, nos viene dado por la expresión:
Sea la función: a) (2 puntos) Dibuje su gráfica y, a la vista de ella, estudie monotonía y extremos.
Calcule las funciones derivadas de las siguientes:
a) (1 punto) ; b) (1 punto) ; c) (1 punto) ;
a) (1.5 puntos) Dada la función
Un agricultor comprueba que si el precio al que vende cada caja de fresas es "x" euros, su beneficio diario, en euros, será:
Se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 800 pta./m. y la de los otros lados 100 pta./m. Hallar el área del campo de mayor superficie que puede cercarse con 288.000 pta.
Aprovechando como hipotenusa una pared de
El alcalde de un pueblo quiere cercar un recinto rectangular cerrado para celebrar las fiestas. Para ello aprovecha una tapia existente como uno de los lados y dispone de 300 m. de tela metálica para hacer los otros tres.
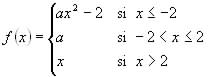
para que 
sea continua en 
.
b) (1 punto) Estudie la continuidad y la derivabilidad de 
cuando 
.
c) (1 punto) Dibuje la gráfica de la función que se obtiene cuando 
.
, donde 
representa los años de vida de la empresa, cuando 
.
a) (2 puntos) Represente gráficamente la función 
, para 
, indicando: dominio, corte con los ejes, asíntotas, crecimiento y decrecimiento.
b) (0.5 puntos) ¿A partir de qué año la empresa deja de tener pérdidas?
c) (0.5 puntos) A medida que transcurre el tiempo, ¿están limitados sus beneficios? En caso afirmativo, ¿cuál es su límite?
.
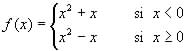b) (0.5 puntos) Estudie su continuidad.
c) (1 punto) Obtenga, si existe, la derivada de f en x = 1/2, x = -1/2 y x = 0.
d) (0.5 puntos) Indique si posee máximos y mínimos relativos y en qué puntos.
.
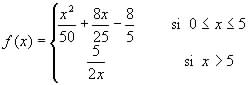a) (1 punto) Represente la función f(x).
b) (0.75 puntos) Halle la inversión que produce máxima ganancia.
c) (0.75 puntos) Halle el valor de la inversión que produce ganancia nula.
d) (0.5 puntos) Razone lo que ocurre con la rentabilidad si la inversión se incrementa indefinidamente.
a) (0.75 puntos) ¿En qué instante alcanza la altura máxima? ¿Cuál es esa altura?
b) (1 punto) Represente gráficamente la función h(t).
c) (0.75 puntos) ¿En qué momento de su caída se encuentra el objeto a 60 metros de altura?
d) (0.5 puntos) ¿En qué instante llega al suelo?
es una parábola de vértice 
que corta al eje de abscisas en los puntos 
y 
. A partir de la gráfica de 
:
a) (1.75 puntos) Estudie el crecimiento y el decrecimiento de 
. ¿Para qué valores de 
se alcanzan los máximos y mínimos relativos?
b) (1.25 puntos) Esboce la forma de la gráfica de una función cuya derivada sea la parábola dada.
a) (1 punto) ¿En qué periodo de tiempo aumenta el consumo? ¿En cuál disminuye?
b) (1 punto) ¿En qué instante se produce el consumo máximo? ¿Y el mínimo?
c) (1 punto) Represente gráficamente la función.
.
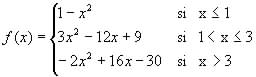b) (1 punto) Estudie su continuidad y derivabilidad.
(
indica logaritmo neperiano de x)
, determine los valores de "b" y "c" sabiendo que dicha función alcanza un máximo relativo en el punto (-1 , 3).
b) (1.5 puntos) Calcule "a" para que el valor mínimo de la función 
sea igual a 8.
.
a) (1 punto) Represente la función precio-beneficio.
b) (1 punto) Indique a qué precio debe vender cada caja de fresas para obtener el máximo beneficio. ¿Cuál será ese beneficio máximo?
c) (1 punto) Determine a qué precios de la caja obtiene pérdidas el agricultor.
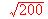m. se desea acotar una superficie triangular de área máxima. ¿Que medidas deberán tener los otros dos lados, (catetos) ?
(1) ¿Podrías indicar las dimensiones del recinto acotado de esa forma cuya área es la mayor posible?
(2) La comisión de fiestas del pueblo ha calculado que para montar las atracciones, pista de baile etc., necesitan 8.000 m2 . Teniendo en cuenta los cálculos realizados en el apartado anterior ¿será suficientemente grande el recinto que quiere preparar el alcalde?