| 10 | 15 | 16 | 20 | 22 | 24 | 30 | 29 | 24 | 5 | 12 | 21 | 2 | 6 | 13 |
Los siguientes datos corresponden a los salarios mensuales, en miles de pesetas, de un grupo de trabajadores en un hospital:100, 110, 120, 150, 90, 80, 115, 110, 125, 600
a) (1 punto) Calcular el porcentaje de salarios de esta muestra que están en el intervalo
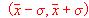 donde
donde 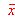 es la media y
es la media y 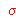 la desviación típica.
la desviación típica.b) (1 punto) Razonar si se deben utilizar estos datos con el propósito de estimar la media salarial de todos los trabajadores españoles.
La Parte II, es el ejercicio nº 5 del tema de probabilidad.
| Vida de la bateria (en meses) | 20 | 22 | 24 | 26 | 28 | 30 |
| Marca A (frec. absoluta) | 5 | 8 | 12 | 15 | 7 | 3 |
| Marca B (frec. absoluta) | 1 | 7 | 18 | 19 | 5 | 0 |
Realice todos los cálculos que considere necesarios para justificar la elección efectuada por la fábrica.
| Superficie | 38 | 45 | 47 | 49 | 45 |
| Producción | 239 | 289 | 335 | 337 | 216 |
(a) Halle la recta deregresión de la producción de lentejas en función de la superficie cultivada.
(b) Si sabemos que en un determinado año la producción fue 420.000 Qm ¿Cuál habrá sido previsiblemente la superficie cultivada durante ese año?
(c) Analice la fiabilidad de la previsión.
(d) Para el periodo 1960-64, calcule la producción mediana y el percentil 60 de la superficie. Razone la respuesta.
Las notas de matemáticas y Física de un grupo de alumnos son las siguientes
| Matemáticas | 2 | 3 | 1 | 7 | 7 | 6 | 8 | 9 |
| Física | 2 | 4 | 2 | 8 | 9 | 6 | 8 | 9 |
a) (1 punto) Representar la nube de puntos y, sobre ella , razonar si hay correlación lineal significativa, y de qué signo, entre las calificaciones de Matemíticas y las de Física.
b) (1 punto) Razonar, sin usar la nube de puntos, si hay una buena correlación.
La Parte I, es el ejercicio nº 4 del tema de Probabilidad.
| Inversión | 14 | 16 | 15 | 16 | 18 | 20 | 21 |
| Rendimiento | 8 | 8 | 7 | 8 | 7 | 9 | 9 |
a) Cuantifique e interprete el coeficiente de correlación lineal.
b) Analice la fiabilidad de las posibles predicciones.
| X | -2 | -1 | 0 | 1 | 2 | 3 |
| Y | -7 | -4 | 1 | 2 | 5 | 8 |
correspondiente a una muestra de una cierta población,
a) (1 punto) Calcule el coeficiente de correlación lineal e interprételo.
b) (1 punto) Dibuje la nube de puntos asociada a la muestra y, a partir de ella, justifique la conclusión obtenida en el apartado anterior.
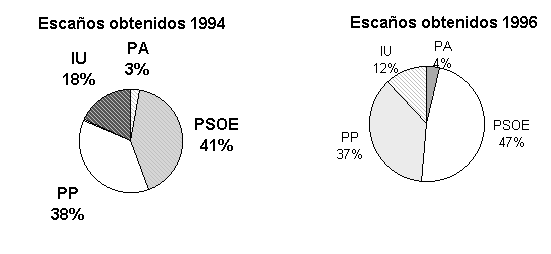
a) (1 punto) Represente estos resultados mediante otro procedimiento gráfico.
b) (1 punto) Dibuje la nube de puntos que se obtiene al representar, por cada partido en abcisas el número de escaños obtenidos en 1994 y en ordenadas el número de escaños obtenidos en 1996. Cuantifique la intensidad de la interrelación lineal existente entre ambas variables
Dada la siguiente distribución estadística bidimensional
| x | 0 | 0 | 2 | k |
| y | 0 | 2 | 0 | 2 |
a) (1 punto) Calcule el valor de k para que el coeficiente de correlación lineal se nulo.
b) (1 punto) A la vista de la distribución y sin desarrollos algebraicos, justifique si puede existir algún valor de k que haga que el coeficiente de correlación lineal sea igual a uno.
La siguiente tabla recoge el número de horas dedicada a preparar la tercera evaluación de Matemáticas y la calificación obtenida en el examen por los alumnos de una muestra.:
| Horas de estudio | 20 | 16 | 34 | 23 | 27 | 32 |
| Calificación del examen | 64 | 61 | 84 | 70 | 88 | 92 |
a) (1,5 puntos) Cuantifique e interprete el coeficiente de correlación lineal. b) (0,5 puntos) Analice la fiabilidad de las posibles predicciones.