ProbabilidadLOGSE

PROBABILIDAD LOGSE

Se lanza un par de dados.
a) Construya el espacio muestral de este experimento aleatorio. b) Si los números resultantes son diferentes, construya el espacio muestral asociado a esta situación y obtenga la probabilidad de que la suma de los números obtenidos sea impar.
Se lanzan dos dados. Uno de ellos es normal y el otro tiene marcado en lugar del seis un uno.
a) Construya el espacio muestral asociado al experimento. b) Halle la probabilidad de obtener una suma igual a 7.
De una baraja española de 40 cartas se extrae una al azar. ¿Cuál es la probabilidad de que sea bastos o menor que cinco?
En una urna hay dos bolas blancas y 1 negra. Si se considera el siguiente experimento aleatorio "Se extrae una bola al azar. Se observa su color y se devuelve a la urna". Calcula la probabilidad de que en dos extracciones se obtengan:
a) 2 bolas blancas.
b) 1 bola blanca y 1 negra.
c) 2 bolas negras.
Se escuchan tres discos y se vuelven a guardar al azar. ¿Cuál es la probabilidad de que al menos uno de los discos haya sido guardado en el envoltorio que le correspondía?
Tomamos cuatro cartas diferentes de una baraja, dos cincos, un seis y un siete. Las cartas se ponen boca abajo sobre una mesa y las mezclamos al azar. Determina la probabilidad de que al darles la vuelta, todas las cartas estén ordenadas en orden creciente, si los dos cincos son indistinguibles.
Dados los sucesos A y B, se sabe que

donde representan respectivamente los sucesos contrarios de A y B .
a) Calcule la probabilidad de que ocurra sólo uno de los sucesosA A y B, b) Compruebe si los sucesos Ay B son independientes
De una urna con cinco bolas, dos blanca y tres negras, extraemos dos bolas sin reemplazamiento. Calcula la probabilidad de cada uno de los siguientes sucesos:
a) A = Las dos bolas extraídas son del mismo color.
b) B = Extraemos al menos una bola blanca.
Lanzamos un dado de seis caras, numeradas de 1 al 6, dos veces consecutivas.
a) Calcula la probabilidad de que la suma de los resultados sea igual a 4.
b) Calcula la probabilidad de que en el primer lanzamiento haya salido un 1, sabiendo que la suma es 4
Si se elige al azar una permutación de las cifras 1, 2, 3, 4, 5, ¿cuál es la probabilidad de que no encontremos cifras impares juntas?
Tiramos una moneda perfecta cien veces. Hacemos la predicción de que saldrán un número de caras comprendido entre 44 y 56. Calcula la probabilidad de no acertar.
Se considera una célula en el instante t = 0. En el instante t = 1 la célula puede: o bien reproducirse, dividiéndose en dos, con probabilidad 3/4; o bien morir, con probabilidad 1/4. Si la célula se divide, entonces, en el tiempo t = 2 cada uno de sus dos descendientes puede también subdividirse o morir, con las mismas probabilidades de antes, independientemente uno de otro.
a) ¿Cuántas células es posible que haya en el tiempo t = 2?
b) ¿Con qué probabilidad?
En un dado trucado, la probabilidad de sacar un 6 es doble que la de cualquiera de los restantes valores. Se lanza el dado 20 veces. ¿Cuál es la probabilidad de que salga 6 más de 15 veces?
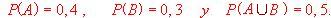
De los sucesos A y B de un experimento aleatorio, se sabe que:

a) Calcule
b) Calcule
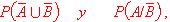
donde 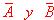representan los sucesos complementarios de A y B.
La caja A contiene 8 pilas de las cuales 3 están descargadas y la caja B contiene 5 pilas de las cuales 2 están descargadas. Se saca al azar, una pila de cada caja.
a) ¿Cuál es la probabilidad de que ambas pilas estén descargadas? b) ¿Cuál es la probabilidad de que una pila esté descargada y la otra no?
Supongamos que, tras una encuesta realizada en la población andaluza, se ha concluido que si se elige al azar un andaluz la probabilidad de que esté a favor de la retransmisión de partidos de fútbol es 0,8 , la de que esté a favor de la existencia de canales de TV de pago es 0,4 y la de que esté a favor de la retransmisión de partidos de fútbol y también de la existencia de canales de pago es 0,3.
a) Calcular la probabilidad de que un andaluz esté a favor de la retransmisión de partidos de fútbol o de que esté a favor de la existencia de canales de televisión de pago.
b) Calcular la probabilidad de que un andaluz ni esté a favor de la retransmisión de partidos de fútbol ni de la existencia de canales de televisión de pago.
En un examen de sociología, un alumno sólo ha estudiado 15 temas de los 25 que contiene el cuestionario. El examen consiste en contestar a dos temas extraídos al azar del total . Hallar la probabilidad de que los dos temas sean de los que el alumno ha estudiado.
El temario de una oposición consta de 100 temas. En el momento del examen se sortean dos y el opositor debe responder obligatoriamente a los dos temas que le han tocado en suerte. Calcular cuántos temas, como mínimo, debe estudiar un opositor para que la probabilidad de saberse los dos temas que le toquen sea superior a 0,5.
Un examen consiste en elegir al azar dos temas de entre los diez del programa y desarrollar uno.
a) ¿Qué probabilidad tienen un alumno, que sabe seis temas, de aprobar el examen?
b) ¿Qué probabilidad tiene el mismo alumno de saberse uno de los dos temas elegidos y el otro no?
Un estudiante se presenta a un examen tipo test compuesto por cien preguntas, cada una de las cuales va acompañada de cuatro respuestas (y sólo una es correcta).
Sesenta de las preguntas corresponden a la parte del programa que el estudiante ha preparado y en las que tiene una probabilidad del 80% de contestar acertadamente. En las preguntas restantes, señalará al azar una de las cuatro respuestas.
Si se elige al azar una de las preguntas, ¿cuál es la probabilidad de que su respuesta sea correcta?
Se considera el experimento aleatorio de lanzar dos dados y anotar el resultado de la tirada.
a) (1.5 puntos) Represente el espacio muestral y los sucesos "sacar al menos un seis" y "sacar suma par".
b) Halle la probabilidad del suceso "los números de los dos dados son diferentes".
c) ¿Son independientes los sucesos "sacar suma par" y "sacar al menos un seis"
Una empresa monta televisores con piezas procedentes de la fábricas F o G. En el primer caso, la probabilidad de que el televisor no tenga averías en cinco años es 0,9 y en el segundo caso, 0,7. El 40% de los televisores se montan con piezas de la fabrica F. Halle la probabilidad de que un televisor, que no ha tenido averías durante cinco años, se haya montado con piezas de la fabrica G.
La probabilidad de que una persona adquiera en una librería un diario es de 0,6; la probabilidad de que no adquiera una revista es de 0,3; la probabilidad de que adquiera una revista dado que ya ha adquirido un diario es 0,2.
Calcule la probabilidad de los siguientes sucesos:
a) Que no adquiera un diario cuando ha adquirido una revista.
b) Que no adquiera una revista cuando ha adquirido un diario.
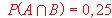Sean A y B dos sucesos, tales que P(A) = 0,5, P(B) = 0,6 y .
a) ¿Son A y B independientes? Calcule
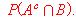
b) Calcule las probabilidades de los sucesos A / B (A condicionado a B) y A /B^c (A condicionado al suceso contrario de B).
La probabilidad de que tenga lugar el contrario de un suceso A es 1/3, la probabilidad de un suceso B es 3/4 y la probabilidad de que ocurran a la vez los sucesos A y B es 5/8. Determinar:
ii) Probabilidad de que se verifique el suceso A o el suceso B.
iii) Probabilidad de que no se verifique A y no se verifique B.
iv) Probabilidad de que ocurra A sabiendo que se ha verificado B.
v) Independencia de los sucesos a y B.
Para tratar cierta enfermedad se dispone de dos medicamentos, con efectos independientes entre si, cuyas probabilidades de sanar a un paciente son respectivamente 1/2 y 1/3. Se administran los dos medicamentos a tres enfermos.
a) Halle la probabilidad de que al menos uno de ellos se cure.
b) Halle le probabilidad de que al menos uno de ellos no se cure.
Se sabe que en una cierta población, la probabilidad de que un hombre esté en paro vale 0,15 y la probabilidad de que una mujer esté en paro vale 0,25. Si la proporción de personas de cada sexo es la misma, calcule las probabilidades de los siguientes sucesos:
a) Una persona elegida al azar está en paro.
b) Que sea un hombre, si se sabe que no está en paro.
Si se escoge un número al azar en la guía telefónica de cierta ciudad española, la probabilidad de que figure a nombre de un hombre es 0,7 y que figure a nombre de una mujer es 0,3. En dicha ciudad, la probabilidad de que un hombre trabaje es 0,8 y de que lo haga una mujer es 0,7. Se elige un número de teléfono al azar.
a) ¿Cuál es la probabilidad de que corresponda a una persona que trabaja?
b) ¿Cuál es la probabilidad de que corresponda a un hombre, sabiendo que pertenece a una persona que trabaja?
En una ciudad se publican dos periódicos, A y B. La probabilidad de que una persona lea el periódicoA es 0,1, la probabilidad de que lea el B es 0,1 y la probabilidad de que lea ambos es 0,02.
a) Calcule la probabilidad de que una persona no lea ningún periódico.
b) Calcule la probabilidad de que una persona que ha leído algún de los dos periódicos lea también el otro
Se sabe que, en una cierta población, la probabilidad de que un hombre tenga estudios universitarios es 0,30 y que la probabilidad de que una mujer tenga estudios universitarios es 0,25. Si los hombres representan el 48% de la población, calcule las probabilidades de los siguientes sucesos:
a) Una persona elegida al azar posee estudios universitarios.
b) Que sea hombre una persona de la que se sabe que no posee estudios universitarios.
Se tienen dos urnas U₁ y U₂ cuyo contenido en bolas rojas, azules y verdes es; en la urna U₁ 4 bolas azules, 3 bolas rojas y 3 verdes, en la urna U₂ 4 rojas, 5 azules y una verde. Se lanzan tres monedas y si se obtienen exactamente dos caras se extrae una bola de la urna U₁, en otro caso se extrae de la urna U₂.
Se pide:
i) Hacer un diagrama para el experimento aleatorio de lanzar tres monedas.
ii) Calcular la probabilidad de que la bola extraída sea azul.
En un centro escolar existen tres grupos de 2º de bachillerato LOGSE. El primero esta compuesto por 10 alumnos de los que 7 prefieren la música "moderna", 2 prefieren la "clásica" y 1 que no le gusta la música. En el segundo compuesto por 12 alumnos, la distribución de preferencias es de 5 , 7 y 0 respectivamente; y en el tercero, formado por 14 alumnos, la distribución e preferencias es de 6, 6 y 2 respectivamente. Se elige un grupo al azar y se regalan dos entradas para un concierto de música clásica a dos alumnos seleccionados al azar.
a) Halle la probabilidad de que las entradas se regalen en el primer grupo.
b) Halle la probabilidad de que los dos alumnos elegidos sean aficionados a la música moderna.
c) Si los dos alumnos agraciados son efectivamente aficionados a la música clásica. ¿Cuál es la probabilidad de que procedan del primer grupo?
a) Explica qué quiere decir que dos sucesos son independientes y qué quiere decir que son incompatibles.
¿Dos sucesos con probabilidades no nulas pueden ser independientes e incompatibles a la vez? Justifica la respuesta.
b) Calcula la probabilidad P(AUB) sabiendo que P(A) = 0,3, P(B) = 0,5 y P(A/B) = 0,2.
En un supermercado, el 70% de las compras las realizan las mujeres; de las compras realizadas por éstas, el 80% supera las 2000 ptas., mientras que de las compras realizadas por hombres sólo el 30% supera esa cantidad.
1. (1 punto) Elegido un ticket de compra al azar, ¿cuál es la probabilidad de que supere las 2000 ptas.?
2. (1 punto) Si se sabe que un ticket de compra no supera las 2000 ptas., ¿cuál es la probabilidad de que la compra haya sido hecha por una mujer?
Una experiencia aleatoria consiste en preguntar a tres personas distintas, elegidas al azar, si son partidarias o no de consumir un determinado producto.
1. (1 punto) Escriba el espacio muestral asociado a dicho experimento, utilizando la letra "s" para las respuestas afirmativas y la "n" para las negativas.
2. (0.5 puntos) ¿Qué elementos del espacio muestral anterior constituyen el suceso "al menos dos de las personas son partidarias de consumir el producto"?
3. (0.5 puntos) Describa el suceso contrario de "más de unapersona es partidaria de consumir el producto".
De los tornillos que se producen en una fábrica, el 60% son producidos por la máquina A y el resto por la máquina B. Supóngase que el 12% de los tornillos producidos por A son defectuosos, y que el 8% de los producidos por B son defectuosos. a) Elegido, al azar, un tornillo producido por esa fábrica, ¿cuál es la probabilidad de que sea defectuoso? b) Se elige al azar un tornillo y resulta que es defectuoso, ¿cuál es la probabilidad de que haya sido producido por la máquina A?
Una fábrica tiene tres máquinas, A, B y C, que producen tornillos. Del total detornillos se producen, respectivamente, el 50%, el 30% y el 20%. La máquina A produce un 5% de tornillos defectuosos, la B un 4% y la C, un 2%.
c) Calcula la probabilidad de que un tornillo, elegido al azar, sea defectuosos. (1 punto).
d) Si un tornillo elegido al azar resulta defectuoso, calcula la probabilidad de que lo haya producido la máquina C. (1,5 puntos).
En un estudio realizado en cierta universidad se ha determinado que un 20% de sus estudiantes no utiliza los transportes públicos para acudir a sus clases y que un 65% de los estudiantes que utiliza los transportes públicos, también hace uso del comedor universitario. Calcula la probabilidad de que seleccionado al azar un estudiante en esa universidad, resulte ser usuario de los transportes públicos y del comedor universitario. Justifica la respuesta.
Se dispone de una baraja española de 40 cartas. Se saca una carta al azar y, sin devolverla a la baraja, se saca otra, también al azar.
1. (1 punto) Calcule la probabilidad de que ninguna de las cartas extraídas sea una figura (es decir, ni sota, ni caballo, ni rey).
2. (1 punto) Sabiendo que la segunda carta extraída no ha sido una figura, calcule la probabilidad de que tampoco lo fuera la primera.
La probabilidad de que un conductor no lleve la rueda de repuesto es 0.13 y la de que no lleve lámparas de repuesto es de 0.37. Se sabe que el 60% de los conductores llevan ambos repuestos.
1. (1 punto) Calcule la probabilidad de que un conductor no lleve alguno de los dos repuestos señalados.
2. (1 punto) ¿Son independientes los sucesos "llevar rueda de repuesto" y "llevar lámparas de repuesto"?
Tenemos tres cajas, una verde, una roja y una amarilla y, en cada caja, hay una moneda. La de la caja verde está trucada y la probabilidad de que salga cara es doble de la probabilidad de que salga cruz; la moneda de la caja roja tiene dos caras y la de la caja amarilla no está trucada. Se toma una caja al azar y se lanza la moneda que está en la caja. Calcula razonadamente:
c) La probabilidad de que salga cara. (5 puntos).
d) La probabilidad de que, sabiendo que ha salido cara, se haya lanzado la moneda de la caja roja. (5 puntos).
El 25% de las familias de cierta comunidad autónoma española no sale fuera de la misma durante las vacaciones de verano. El 65% veranea por el resto de España y el 10% restante se va al extranjero. De los que se quedan en su comunidad, sólo un 10% no utiliza el coche en sus desplazamientos. Esta cantidad aumenta al 30% entre los que salen por el resto de España, y al 90% entre los que viajan al extranjero.
a) calcula el porcentaje de familias de esa comunidad que utiliza el coche en sus desplazamientos de vacaciones de verano.
b) Una familia no usa el coche en sus vacaciones de verano. ¿Cuál es la probabilidad de que salga de su comunidad moviéndose por el resto de España?
En un determinado lugar hay tres lugares de diversión a los que suelen ir un grupo de amigos. Las probabilidades de que vayan al primero, segundo o tercero son , respectivamente, 0,3, 0,5 y 0,7. Hallar la probabilidad de que el grupo de amigos vaya :
1. Solamente a uno de los lugares.
2. Únicamente a dos de los lugares.
3. A los tres lugares.
Se reparten unas invitaciones sabiendo que sólo el 40% asistirán al acto. Se selecciona al azar 10 invitados. Calcular:
a) La probabilidad de que sólo tres de esos diez invitados acudan al acto.
b) La probabilidad de que acudan más de tres de los diez.
En un instituto se ofertan tres modalidades excluyentes, A, B y C, y dos idiomas excluyentes, inglés y francés. La modalidad A es elegida por un 50% de los alumnos, la B por un 30% y la C por un 20%.
También se conoce que han elegido inglés el 80% de los alumnos de la modalidad A, el 90% de la modalidad B y el 75% de la C, habiendo elegido francés el resto de los alumnos.
a) ¿Qué porcentaje de estudiantes del instituto ha elegido francés?
b) Si se elige al azar un estudiante de francés, ¿cuál es la probabilidad de que sea de la modalidad A?
A partir de la información que recoge las pautas de consumo de cigarrillos de la población femenina, las autoridades sanitarias desean adoptar las medidas oportunas con objeto de reducir dicho consumo.

Consumo de cigarrrillos diarios 0-5 5-10 10-15 15-20 20-25

Población femenina (miles de hab.) 2 10 15 7 2

a) Determinar el consumo más frecuente.
b) Calcule el consumo medio y su desviación típica.
c) La media y la desviación típica del consumo masculino ha sido 14 y 4. respectivamente. Un consumo de 17 cigarrillos, ¿en qué población se destaca más?; ¿por qué?
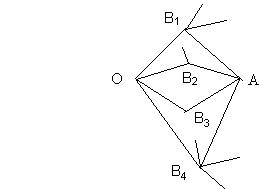
Supongamos que un móvil sale del punto O y elige un camino al azar (véase la figura). En cada cruce, elige también un camino al azar. ¿Cuál es la probabilidad de que llegue a A?
Un ratón huye de un gato, puede entrar por cada uno de los callejones A , B ó C. En cada uno de ellos el gato puede alcanzarlo o no. Se dan las siguientes probabilidades P(entre por A) = P(A) = 0,3 ; P(B) = 0,5 ; P(C) = 0,2.
P(Lo cace habiendo entrado en A) = P(+/A) = 0,4 ; P(+/B) = 0,6 y P(+/C) = 0,1
Calcular la probabilidad de que el gato cace al ratón.
En una casa hay tres llaveros A, B y C, el primero con tres llaves, el segundo con cinco llaves y el tercero con siete, de las que sólo una de cada llavero abre la puerta del trastero. Se escoge al azar un llavero y de él una llave para intentar abrir el trastero. Se pide :
a) ¿Cuál es la probabilidad de que se acierte con la llave?
b) ¿Cuál será la probabilidad de que el llavero escogido sea el tercero y la llave no abra?
Un vehículo es sometido a una inspección técnica. En el proceso de inspección tiene que pasar por tres controles: A, B y C (en este orden). Por la experiencia acumulada, se sabe que el control A informa negativamente en el 15% de los casos o bien pasa el vehículo al control B, quien a su vez, informa negativamente en el 8% de los casos o bien pasa el vehículo al control C. Finalmente, C informa negativamente con probabilidad 0,02 o emite informe favorable. Cuando un control emite informe negativo el vehículo es declarado "No apto para circular". ¿Cuál será la probabilidad de que un vehículo sometido a dicha inspección técnica sea declarado "No apto para circular"? Justificar la respuesta.
De una baraja de 48 cartas se extraen simultáneamente dos de ellas. Calcular la probabilidad de que :
a) Las dos sean copas.
b) Al menos una sea copas.
c) Una sea copas y la otra espadas.
Se lanza un dado 4 veces y se considera la variable aleatoria X, que indica el número de veces que se obtiene una puntuación divisible entre 3.
Establecer la distribución de probabilidad y la función de distribución de la variable X y representarlas gráficamente.
¿Qué tablas, entre las siguientes, podrían ser la distribución de probabilidad de una cierta variable aleatoria X? Razonar la respuesta.
Hallar la probabilidad de que una familia con 4 hijos tenga
a) al menos 1 varón.
b) al menos 2 hembras.
Se sabe que la probabilidad de que un habitante de cierto país sea rubio es 0,4, y la de que tenga ojos negros, 0,3. Calcular las probabilidades de que:
a) Elegida una persona sea rubia y de ojos negros.
b) Elegida una persona, no sea rubia o tenga los ojos negros.
c) Elegidas tres personas, sean rubias.
d) Elegidas dos personas, sean rubias o tengan los ojos negros.
En un monedero hay 5 monedas: una de peseta, dos de duro, y dos de cinco duros. Sacamos una moneda al azar y anotamos su valor en pesetas. Establecer las funciones de probabilidad y de distribución de la correspondiente variable aleatoria y representarlas gráficamente.
El 5% de los habitantes de una gran ciudad poseen titulo universitario. ¿Cuál es la probabilidad de que elegidas al azar 50 de dichas personas haya a lo sumo 4 con titulación universitaria?
El 5% de los habitantes de una gran ciudad son analfabetos. ¿Cuál es la probabilidad de que elegidas al azar 50 de dichas personas haya a lo sumo 4 que sean analfabetas ?
La probabilidad de nacimientos de niños varones en España es de 51'7% . Hallar la probabilidad de que una familia de 5 hijos tenga:
a) Por lo menos una niña.
b) Por lo menos un niño.
Calcular la probabilidad de que en una colectividad de 30 individuos 10 hayan nacido el día de Navidad.
Una caja contiene 5 lamparas eléctricas. Se sabe que dos de ellas están defectuosas. Si probamos una tras otra hasta localizar las dos defectuosas, ¿cual es la probabilidad de suspender el proceso en la tercera prueba?
Es conocido que en cierto país la probabilidad de que un hombre de 25 años llegue a los 75 años, es de 0,8. Si elegimos a 3 hombres de 25 años de dicho país, calcular la probabilidad de que:
a). Sólo uno llegue a los 75 años.
b). Al menos uno llegue a los 75 años.
Explica cual es la fórmula de la probabilidad de que al lanzar 3 monedas se obtengan " x " caras. Aplicando dicha fórmula se pide:
a) ¿Cuál es la probabilidad de obtener 1 cara?
b) ¿Cuál es la probabilidad de obtener 3 caras?
c) Si sabemos que se ha obtenido un número impar de caras ¿cuál es la probabilidad de que el número de caras obtenidas sea 1?
El 4% de los frigoríficos fabricados en determinada cadena de montaje son defectuosos. Si la producción mensual de dicha cadena es de 2.000 frigoríficos, ¿cuál es la probabilidad de que en un mes cualquiera el número de frigoríficos defectuosos esté comprendido entre 60 y 100
Se admite que la probabilidad de que una cierta vacuna produzca reacción alérgica es de 0,0001. ¿Qué probabilidad hay de que en una campaña de vacunación extendida a 26.000 personas, se den más de 4 casos alérgicos?
En cierta población de varones se ha determinado que el porcentaje de fumadores es del 40%. Si 10 personas son seleccionadas al azar en dicha población, calcular : a) La probabilidad de que no haya entre ellas ningún fumador. b) La probabilidad de que al menos haya entre ellas un fumador. c) El número esperado de fumadores en esas 10 personas. Justificar las respuestas.
El Ministerio de Educación y Ciencia ha determinado que el 30% de los alumnos que inician un determinado nivel sufren el llamado fracaso escolar. Elegidos 8 alumnos al azar de ese nivel, hallar : a) La probabilidad de que ninguno fracase escolarmente , b) La probabilidad de que fracase la mitad. c) La media y la varianza de la distribución.
El 75% de la población considera que los tratamientos de psicoterapia son caros. Elegidos una muestra al azar formada por 6 individuos, hallar : a) La probabilidad de que los 6 los consideren caros. b) La probabilidad de que ninguno los considere caros. c) La probabilidad que al menos dos lo consideren caros.
En una celebración familiar, 15 personas (9 adultos y 6 niños) comieron alimentos contaminados con cierta bacteria. Es conocido que una vez se entra en contacto con esa bacteria, hay un 25% de posibilidades de que un adulto manifieste cierta enfermedad intestinal y un 40% de que la manifieste un niño. a) ¿Cuál es la probabilidad de que no más de 3 adultos manifiesten la enfermedad? b) ¿Cuál es la probabilidad de que exactamente 2 niños manifiesten la enfermedad? c) ¿Qué número de personas (entre las 15) cabe esperar manifiesten esa enfermedad?
Se ha comprobado que determinada prueba cultural es superada por el 70 % de las personas con estudios de grado medio y por el 55% de las personas con estudios primarios. Un total de 10 personas (6 con estudios de grado medio y 4 con estudios primarios) realizan dicha prueba cultural. Se pide: a) La probabilidad de que exactamente 4 de las personas con estudio de grado medio superen la prueba. b) La probabilidad de que al menos 1 de las personas con estudios primarios superen la prueba. c) Si consideramos la variable "Número de personas que superan la prueba entre las 10 que la realizan", ¿seguiría dicha variable un modelo binomial de probabilidad? Justificar las respuestas.
En la fabricación en serie de bombillas en cierta fábrica, se estima que cada partida de 1.000, cinco son defectuosas. Si en un año se han fabricado 50.000 bombillas , ¿cuántas cabe esperar que presenten defectos? ¿cuál es la varianza y la distribución típica de la distribución?
Cuando se administra a una madre sifilítica cantidad suficiente de penicilina en el curso del embarazo, se tiene la probabilidad de 0'95 de que la criatura nazca sana. Determinar la probabilidad de que en un grupo de 6 madres sifilíticas que están embarazadas y se les suministra penicilina regularmente a) 4 de ellas tengan criaturas sanas. b) 4 de ellas tengan criaturas no sanas.
Si el 20% de los cerrojos producidos por una maquina son defectuosos, determinar la probabilidad de que de 4 cerrojos elegidos al azar, (a) 1 sea defectuoso. (b) a lo más 2 sean defectuosos.
En una factoría se produce un nuevo objeto formado por 4 piezas. En la producción de 1.000 de tales objetos se han obtenido las siguientes frecuencias de objetos defectuosos:

Componentes defectuosos 0 1 2 3 4

Nº de juguetes 767 172 50 8 3

Ajustar una distribución binomial y calcular la probabilidad de que, elegido un juguete al azar, tenga exactamente un componente defectuoso.
Una moneda fue lanzada al aire 1000 series de 5 veces cada serie, y se observo el número de caras de cada serie:

nº de caras 0 1 2 3 4 5

nº de series 38 144 342 287 164 25

Ajustar una distribución binomial a estos datos.
Se ha determinado que la probabilidad de que cierta semilla germine, es de 3/4 si es plantada en terreno húmedo, y de 1/5 si es plantada en terreno seco. Un agricultor planta 12 de tales semillas en terreno húmedo y 15 en terreno seco. Contestar, justificando la respuesta: a) ¿Qué probabilidad hay de que germine 8 de las 12 semillas plantadas en terreno húmedo?. b) ¿Qué probabilidad hay de que no germine ninguna de las 15 semillas plantadas en terreno seco?. c) ¿Qué número total, (entre los dos terrenos), de semillas cabe esperar que germinen?. d) ¿La variable "Nº de semillas que germinan entre las 27 plantadas", seguiría un modelo Binomial de probabilidad
La duración en segundos, de los discos que ponen en cierta emisora de radio sigue una distribución Normal de media 180 sg. y desviación 30 sg.
a) ¿Qué porcentaje de discos tendrá una duración comprendida entre 170 y 200 segundos?
b) ¿Cuál es la probabilidad de que un disco elegido al azar dure más de 180 sg.?
¿Que relación guardan tres curvas de distribución normal con la misma media y distinta desviaciones? ¿ y con la misma desviación típica y distintas medias? Justifiquese la respuesta.
Se ha aplicado a 300 alumnos de un instituto un test de memorización y se ha observado que los resultados se distribuyen normalmente, con media 30 y desviación típica 12. Responder razonadamente las siguientes cuestiones:
a) ¿Qué porcentaje de alumnos tendrá una puntuación, en dicho test, comprendida entre 20 y 30?
b) ¿Cuántos alumnos tendrán puntuación superior a 42?
Se llama cociente intelectual (C.I.) al coeficiente entre la edad mental y la edad real. Se sabe que la distribución del C.I. se distribuye normalmente con media 0,95 y desviación típica 0,22. En una población con 2.600 personas se desea saber:
a) ¿Cuántas tendrán un C.I. superior a 1,37?
b) ¿Cuántas tendrán un C.I. inferior a 0,07?
c) ¿Cuántas tendrán un C.I. entre 0,8 y 1,15?
Se sabe que las calificaciones del profesor A se distribuyen N(4'4 , 2'5) y las del profesor B, N(4'8 , 0'9). Sabiendo que ambos profesores aprueban al alumno cuando su calificación es igual o superior a 5, ¿con cual de ellos es más fácil aprobar?
El peso de los toros de determinada ganadería se distribuye como una distribución normal 500 kg. de media y 45 kg. de desviación típica. Si la ganadería 2.000 toros,
a) ¿Cuántos pesarán más de 540 kg.?
b) ¿Cuántos pesarán menos de 480 kg.?
c) ¿Cuántos pesarán entre 490 y 510 kg.?
Tras aplicar un examen a un gran colectivo de estudiantes, se comprobó que las calificaciones obtenidas se ajustaban bastante a una distribución normal. La calificación media de la distribución fue 5,8 y la distribución típica 1. Elegido al azar un estudiante, ¿cual es la probabilidad de que su calificación esté comprendida entre 6,7 y 6,85
La vida media de una cierta población (áfrica?) es de 45 años, con una desviación típica de 5 años. Calcular la probabilidad de que elegido un elemento de esta población al azar, tenga más de 52 años. (se supone que la vida de una población sigue una ley normal).
Supongamos que la distribución de estaturas de una población es una distribución normal de media 160 cm. y desviación típica 10 cm. Hallar la probabilidad de que una persona elegida al azar tenga una estatura comprendida entre 166,5 y 167,5 cm.
Una población de personas sigue una ley normal en la distribución de sus pesos, se sabe que el 90% de la población pesa más de 50 kg. y que el 80% pesan menos de 80 kg. Calcular la media y desviación típica de la distribución de pesos.
La presión sanguínea de ciertos enfermos sigue una ley normal de media 90 mm. Hg y de desviación típica 12 mm. Hg. Hallar la probabilidad de que elegido un paciente al azar:
a) Su presión sea mayor que 115 mm. Hg.
b) Su presión este comprendida entre 80 y 110 mm. Hg.
Los estudiantes de una Universidad fueron sometidos a un test de inteligencia. Suponiendo que las puntuaciones alcanzadas siguen una ley normal con media igual a 100 puntos y desviación típica igual a 10 puntos, se pide hallar las probabilidades de que: (a) un estudiante obtenga más de 120 puntos, (b) un estudiante obtenga menos de 80 puntos.
El peso en toneladas de los rollos de acero fabricados en una planta se distribuyen según una ley normal N(10 ; 0,5). Sólo se admiten los rollos con peso comprendido entre 9,5 y 11 toneladas. ¿Cuál es la probabilidad de rechazar un rollo dado?
Se ha aplicado a 300 alumnos un test y se ha obtenido que los resultados se distribuyen normalmente con media 30 y desviación típica 12.
a) ¿Qué porcentaje de alumnos tendrá una puntuación comprendida entre 20 y 30?
b) ¿ Cuántos alumnos tendrán puntuación mayor de 42?
Se ha comprobado que el Tiempo de tramitación , (en días) , de cierta documentación, sigue una N(12 , 2) en la oficina A, y una N(12 , 1) en la oficina B. Indicar, justificando la respuesta, en cuál de las dos oficinas, es más probable que la documentación tarde en tramitarse : a) mas de 12 días. b) menos de 10 días.
La cantidad de sustancia S contenida en una dosis de cierta vacuna se distribuye según un modelo Normal de probabilidad con una media de 50 unidades. Se ha comprobado que la vacuna surte efecto, (inmuniza), si la dosis administrada contiene una cantidad de S comprendida entre 46 y 54 unidades. Sabiendo que el 2,5% de las dosis contienen una cantidad de S superior a 54 unidades, a) ¿Qué probabilidad hay de que un individuo, al que se le administre una dósis elegida al azar, no se inmunice? justificar la respuesta. a) aproximadamente ¿cuánto vale la desviación típica?
En una población de deportistas se ha comprobado que el tiempo de recuperación tras determinado esfuerzo físico, sigue un modelo Normal de probabilidad con una media de 5 minutos. Sabiendo que el 2,5% de tales deportistas tardan en recuperarse de ese esfuerzo físico más de 7 minutos, contestar justificando la respuesta : a) ¿Qué porcentaje de deportistas tardan en recuperarse entre 3 y 5 minutos?. b) Aproximadamente, ¿cuál sería la desviación típica?
En una población de estudiantes se ha comprobado que la calificación obtenida en Inglés sigue un modelo Normal de probabilidad con una media de 5 si se ha seguido el método de trabajo A y con una media de 6 si se ha seguido el método de trabajo B. Sabiendo que el 4% de los alumnos que han seguido el método A obtienen una calificación inferior a 3,5 y que el 2% de los alumnos que han seguido el método B superan el 8, contestar razonadamente las respuestas: a). ¿Qué porcentaje de estudiantes adiestrados con el método A no superan la calificación de 6,5? b). ¿Qué porcentaje de estudiantes adiestrados con el método B obtienen calificación comprendida entre 4 y 6?
Cierto fármaco se comercializa en tabletas de 100 mg. En su composición intervienen la sustancia S y se ha comprobado que la cantidad de S por tableta sigue un modelo Normal con media 20 mg y varianza 4 mg².
Sabiendo que una tableta surte efecto para cierta dolencia únicamente si contiene entre 19 y 22 mg de S, se pide: a)¿ Cuál sería la probabilidad de que una tableta no surta efecto para esa dolencia? b) ¿Qué cantidad de S por tableta sería superada por el 67% de la producción?. Justificar la respuestas.
En la ciudad A, la edad de sus 400.000 habitantes sigue una distribución normal de media 41 años y desviación típica 12 años. En la ciudad B, con el doble de habitantes, la edad se distribuye normalmente con media 47 años y desviación típica 8 años.
¿En cuál de las dos ciudades es mayor la proporción de habitantes mayores de 65 años?
¿Cuál de las dos ciudades tiene mayor número de habitantes con edad superior a 65 años?
Una biblioteca pública está organizada en cinco secciones (en el cuadro adjunto se indica el numero de libros existentes en cada sección). Con el objeto de estimar el porcentaje de libros de edición española, se quiere seleccionar una muestra de un 5% del numero total de libros, a través de muestreo estratificado aleatorio, considerando como estratos las secciones.
Determinar el numero de libros que habría que seleccionar en cada sección, si:
a) Consideramos afijación igual. b) Consideramos afijación proporcional.

Sección 1 Sección 2 Sección 3 Sección 4 Sección 5

500

860

1.200

700

740
El peso de los niños varones a las 10 semanas de vida se distribuye según una normal con desviación típica de 87 g. ¿Cuántos datos son suficientes para estimar, con una confianza del 95%, el peso medio de esa población con un error no superior a 15 g.?
El consumo de un cierto producto sigue una distribución normal con varianza 300. A partir de una muestra de tamaño 25 se ha obtenido una media muestral igual a 180. Halle un intervalo de confianza al 95% para la media del consumo.
Los estudiantes de las Universidades de cierto país dedican al estudio un número de horas semanales que sigue una distribución normal de media desconocida y de desviación típica 7 horas.
Calcule cuantos estudiantes deberán seleccionar al azar para determinar el parámetro con una precisión inferior a una hora y con una confianza del
a) 90%
b) 99%
La edad, en años de las personas de una población se distribuye normalmente con media desconocida y varianza 4. ¿Cuál es el tamaño muestral a partir del cual la edad media de la población difiere de la media muestral en menos de 1 año con una confianza del a) 90% ,
b) 99%.?
La talla de los individuos de una población sigue una distribución normal de media y desviación típica 8 cm.
Se han determinado las tallas de 25 individuos, encontrándose una media de 168 cm. Obtenga un intervalo de confianza al 95% para la media de la población.
La media de edad de los alumnos que se presentan a las pruebas de acceso a la Universidad es de 18.1 años y la desviación típica 0.6 años.
1. (1 punto) De los alumnos anteriores se elige, al azar, una muestra de 100, ¿cuál es la probabilidad de que la media de la edad de la muestra esté comprendida entre 17.9 y 18.2 años?
2. (1 punto) ¿Qué tamaño debe tener una muestra de dicha población para que su media esté comprendida entre 17.9 y 18.3 años, con una confianza del 99.5%?
Se ha tomado una muestra aleatoria de 100 individuos a los que se ha medido el nivel de glucosa en sangre, obteniéndose una media muestral de 110 mg/cc. Se sabe que la desviación típica de la población es de 20 mg/cc.
1. (1.5 puntos) Obtenga un intervalo de confianza, al 90%, para el nivel de glucosa en sangre en la población.
2. (0.5 puntos) ¿Qué error máximo se comete con la estimación anterior?
Las ventas mensuales de una tienda de electrodomésticos se distribuyen según una ley normal con desviación típica 90000 ptas. En un estudio estadístico de las ventas realizadas en los últimos 9 meses, se ha encontrado un intervalo de confianza para la media mensual de las ventas, cuyos extremos son 466300 y 583900 ptas.
1. (0.5 puntos) ¿Cuál ha sido la media de las ventas en estos 9 meses?
2. (1.5 puntos) ¿Cuál es el nivel de confianza de ste intervalo?
La media de las estaturas de una muestra aleatoria de 400 personas de una ciudad es 1.75 metros. Se sabe que la estatura de las personas de esa ciudad es una variable aleatoria que sigue una distribución normal con varianza .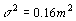
1. (1 punto) Construya un intervalo, de un 95% de confianza, para la media de las estaturas de la población.
2. (1 punto) ¿Cuál sería el mínimo tamaño muestral necesario para que pueda decirse que la verdadera media de las estaturas está a menos de 2 cm. de la media muestral, con una confianza del 90%?
Parte I. Una experiencia aleatoria consiste en preguntar a tres personas distintas elegidas al azar, si son partidarias o no de consumir un determinado producto. a) Escribe el espacio muestral asociado a dicho experimento, utilizando la letra “s” para la respuestas afirmativas y la “n” para las negativas. (1 punto)
b) ¿Qué elementos del espacio muestral anterior constituyen el suceso ”al menos dos de las personas son partidarias de consumir el producto”. (0,5 puntos)
c) Describe el suceso contrario de “más de una persona es partidaria de consumir el producto”. (0,5 puntos)

Parte II. Se ha tomado una muestra aleatoria de 100 individuos a los que se ha medido el nivel de glucosa en sangre, obteniéndose una media muestral de 110 mg/cc. Se sabe que la desviación típica de la población es de 20 mg/cc.
a) Obtén un intervalo de confianza, al 90%, para el nivel de glucosa en sangre en la población. (1,5 puntos)
b) ¿Qué error máximo se comete con la estimación anterior? (0,5 puntos)
Parte I. Ana, Juan y Raúl, que están esperando para realizar una consulta médica, sortean, al azar, el orden en que van a entrar.
a) Calcule la probabilidad de que los dos últimos en entrar sean hombres. (0,75 puntos).
b) Determine si son independientes los sucesos S1 y S2 , siendo:
S1 : “la mujer entra antes que alguno de los hombres”.
S2 : “Los dos hombres entran consecutivamente” (1,25 puntos).

Parte II. Se ha tomado una muestra de los precios de un mismo producto alimenticio en 16 comercios, elegidos al azar en un barrio de una ciudad, y se han encontrado los siguientes precios:
95, 108, 97, 112, 99, 106, 105, 100, 99, 98, 104, 110, 107, 111, 103, 110
Suponiendo que los precios de este producto se distribuyen según una normal de varianza 25 y media desconocida:
a) ¿Cuál es la distribución de la media muestral? (1 punto).
b) Determine el intervalo de confianza, al 95%, para la media poblacional. (1 punto).
En los últimos tiempos, las ventas medias en un comercio rondaban las 120.000 pesetas diarias. Sin embargo, hace unos meses abrió una superficie comercial cerca del mismo. El establecimiento defiende que las ventas medias se mantiene o, incluso, han aumentado, pero no han disminuido.
Para contrastar estadísticamente este supuesto se ha seleccionado una muestra de las ventas diarias realizadas después de la apertura de la superficie comercial.
a) Establecer la hipótesis nula y alternativa.
b) ¿Qué nombre recibe la probabilidad de que el establecimiento concluya erróneamente que las ventas medias han disminuido? Explica cómo se denomina y en qué consiste el otro error posible?
c) El establecimiento ha encargado el estudio a un especialista y en su informe afirma textualmente que “el valor obtenido al realizar el contraste es significativo”, pero el establecimiento no entiende el significado de la frase.
¿Significa que el establecimiento debe concluir que sus ventas medias disminuyeron, o es lo contrario?
La altura de los jóvenes andaluces se distribuye según ley normal de media desconocida y varianza 25 cm . Se ha una muestra aleatoria, y con una confianza del 95%, se ha construido un intervalo para la media poblacional cuya amplitud es 2,45 cm.
a) ¿Cuál ha sido el tamaño de la muestra seleccionada? (1 punto)
b) Determina el límite superior y el inferior del intervalo de confianza si la muestra tomada dio una altura media de 170 cm. (1 punto)
El estudio de un test de satisfacción de usuario que rellenan todos los demandantes de servicios de una gran empresa revela que la nota media que otorgan es de 5,70 puntos con una desviación típica de 0,5. Posteriormente se ha realizado un muestreo a 100 usuarios de la zona de influencia A, y a 49 usuarios de la zona B, obteniéndose puntuaciones medias respectivas de 5,6 y 5,85. Con una confianza del 95% ¿se puede afirmar que las diferencias entre las medias de cada muestra y de la población son debidas al azar, o se puede afirmar que son diferentes la nota media de la población y la de cada muestra? Formula la hipótesis nula y alternativa. Define error de tipo I y error de tipo II.
Se ha aplicado un test de fluidez verbal a 500 alumnos de primero de E.S.O. de un centro de secundaria. Se supone que las puntuaciones obtenidas se distribuyen según una normal de media 80 y desviación típica 12. Se pide:
a) ¿Qué puntuación separa el 25% de los alumnos con menos fluidez verbal?
b) ¿A partir de qué puntuación se encuentra el 25% de los alumnos con mayor fluidez verbal?
Una encuesta realizada sobre 40 aviones comerciales revela que la antigüedad media de estos es de 13,41 años con una desviación típica muestral de 8,28 años. Se pide:
b) ¿Entre qué valores, con un 90% de confianza, se encuentra la auténtica media de la flota comercial?
c) Si se quiere obtener un nivel de confianza del 95% cometiendo el mismo error de estimación que en el apartado anterior y suponiendo también que s=8,28 años, ¿cuántos elementos deberían componer la muestra?
La media de ventas diarias de un vendedor de unos grandes almacenes es de 95.000 pesetas y la desviación típica es 20.000 pesetas. Suponiendo que la distribución de ventas es normal, ¿cuál es la probabilidad de vender más de 125.000 pesetas en un día?
Se conoce que 25 de cada 1.000 objetos elaborados por una empresa son defectuosos.
De qué tamaño conviene tomar una muestra para que la proporción estimada de defectuosos no difiera de la verdadera en más de un 5% con un nivel de confianza de un: 1. 95% 2. 99% 3. 99,9%
En una ciudad el peso de los recién nacidos se ha distribuido según la ley Normal de media =3.100 gramos y desviación típica =150 g.
Halla los parámetros de la distribución que siguen las medias de las muestras de tamaño 100.
a) Un fabricante de medicamentos afirma que cierta medicina cura una enfermedad de la sangre en el 80% de los casos. Los inspectores de sanidad utilizan el medicamento en una muestra de 100 pacientes y deciden aceptar dicha afirmación si se curan 75 o más. Si lo que afirma el fabricante es realmente cierto, ¿cuál es la probabilidad de que los inspectores rechacen dicha afirmación? b) Si en la muestra anterior se curan 60 individuos, con una confianza del 95% ¿cuál es el error máximo cometido al estimar que el porcentaje de efectividad del medicamento es del 60%?
Se supone que la estatura de los chicos de 18 años de cierta población sigue una normal de media 162 cm y desviación típica 12 cm. Se toma una muestra al azar de 100 de esos chicos encuestados y se calcula sus media.
¿Cuál es la probabilidad de que esta media esté entre 159 y 165 cm?
En una determinada población se toma una muestra al azar de 256 personas. De esta muestra, el 20% de las personas lleva gafas graduadas y el 80% restante no.
Calcula el intervalo de confianza aproximada para la proporción de personas
El número de kilogramos diarios de cierto producto que se vende por kilos es una variable aleatoria continua con función de densidad

Si compramos el kilo a 6.000 pesetas y lo vendemos a 10.000 pesetas:
a) ¿Qué porcentaje de días ganaremos más de 40.000 pesetas?
b) ¿Qué media diaria de beneficios se espera obtener?
Un país está habitado por dos grupos étnicos, M y N, que se encuentran en las proporciones 75% y 25%, respectivamente. Se conoce que la talla de los individuos adultos varones es N(m , s ), con m = 170 y s = 5 cm para el grupo M, m = 175 y s = 5 cm para el grupo N. Se conviene en que un individuo es alto si su talla es superior a 180 cm. Se pide:
a) Porcentaje de individuos altos en el grupo M
b) Porcentaje de altos en el grupo N.
c) Porcentaje de altos en el país.
d) Si un individuo es alto, ¿cuál es la probabilidad de que pertenezca al grupo
Se sabe que el peso en kilogramos de los alumnos de bachillerato de Madrid, es una variable aleatoria X que sigue una distribución normal de desviación típica igual a 5 kg.
a) En el caso de considerar muestras de 25 alumnos, ¿qué distribución tiene la variable aleatoria media muestral ?
b) Si se desea que la media de la muestra no difiera en más de 1 kg de la media de población, con probabilidad 0,95; ¿cuántos alumnos se deberían tomar en la muestra?
Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media m = 100 meses y desviación típica s = 12 meses. Determina el mínimo tamaño muestral que garantiza, con una probabilidad de 0,98, que la vida media de los electrodomésticos en dicha muestra se encuentra entre 90 y 110 meses.
Dos variables aleatorias independientes X₁ y X₂ siguen una distribución normal con media m y desviación típica s
1. ¿Qué distribución tiene la variable aleatoria?
2. Si m = 15 y s = 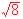, calcula: P(X₁ + X₂> 28)
Estamos realizando una encuesta sobre el nivel de conocimientos generales de los estudiantes de Bachillerato de los diferentes centros de Madrid. Para ello, hemos elegido una muestra aleatoria de 9 de estos estudiantes, a los que le hemos realizado un examen. Las calificaciones obtenidas han sido las siguientes:
7,8 6,5 5,4 7,1 5,0 8,3 5,6 6,6 6,2
Se supone que la variable aleatoria objeto de estudio sigue una distribución normal de desviación típica conocida e igual a 1. Se pide:
a) Un intervalo de confianza al 98% para la media de las calificaciones en el examen.
b) El tamaño mínimo que debería tener la muestra, en el caso de admitir un error máximo de 0,5 puntos, con un nivel de confianza del 95%
Se desea estudiar el gasto semanal de fotocopias, en pesetas, de los estudiantes de bachillerato de Madrid. Para ello, se ha elegido una muestra aleatoria de 9 de estos estudiantes, resultando los valores siguientes para estos gastos:
100 150 90 70 75 105 200 120 80
Se supone, que la variable aleatoria objeto del estudio, sigue una distribución normal de media desconocida y de desviación típica igual a 12. Determínese un intervalo de confianza al 95% para la media del gasto semanal en fotocopias por estudiante.
a) Un fabricante de medicamentos afirma que cierta medicina cura una enfermedad de la sangre en el 80% de los casos. Los inspectores de sanidad utilizan el medicamento en una muestra de 100 pacientes y deciden aceptar dicha afirmación si se curan 75 o más. Si lo que afirma el fabricante es realmente cierto, ¿cuál es la probabilidad de que los inspectores rechacen dicha afirmación?
b) Si en la muestra anterior se curan 60 individuos, con una confianza del 95% ¿cuál es el error máximo cometido al estimar que el porcentaje de efectividad del medicamento es del 60%?
Parte I
Una caja contiene diez tornillos, de los que dos son defectuosos.
a) (1 punto) Si vamos extrayendo tornillos, uno tras otro, hasta localizar los dos defectuosos, ¿cuál es la probabilidad de necesitar exactamente tres extracciones para localizarlos?
b) (1 punto) Si extraemos solo dos tornillos, y el segundo ha resultado ser defectuoso, ¿cuál es la probabilidad de que el primero también lo haya sido?
Parte II
(2 puntos) Según un estudio sociológico, el gasto mensual de los jóvenes españoles durante los fines de semana se distribuye según una ley normal de media pts. y desviación típica pts. Tomamos, al azar, una muestra de 36 jóvenes.
¿Cuál es la probabilidad de que esta muestra tenga un gasto medio comprendido entre pts. y pts?
Parte I
Disponemos de tres dados, uno de los cuales está trucado. La probabilidad de sacar 5 con el dado trucado es 0,25, siendo los otros resultados equiprobables. Se elige un dado al azar y se realiza un lanzamiento con él.
a) (1 punto) Determine la probabilidad de obtener un 2.
b) (1 punto) Dado que ha salido un 2, ¿cuál es la probabilidad de que hayamos elegido el dado trucado?

Parte II
(2 puntos) Sabiendo que la varianza de una ley normal es , determine el nivel de confianza con el que puede decirse que su media está comprendida entre 6,2 y 8,8, si se toma una muestra aleatoria de tamaño 36 de esa ley normal, cuya media muestral es 7,5.
Parte I
En una ciudad el 60 % de sus habitantes son aficionados al fútbol, el 30 % son aficionados al baloncesto y el 25 % a ambos deportes.
a) (0.5 puntos) ¿Son independientes los sucesos "ser aficionado al fútbol" y "ser aficionado al baloncesto"?.
b) (0.75 puntos) Si una persona no es aficionada al fútbol, ¿cuál es la probabilidad de que no sea aficionada al baloncesto?
c) (0.75 puntos) Si una persona no es aficionada al baloncesto, ¿cuál es la probabilidad de que sea aficionada al fútbol?

Parte II
(2 puntos) El periodo de funcionamiento de las bombillas de una determinada marca sigue una distribución normal de media 360 días y desviación típica 40 días.
Queremos elegir una muestra de bombillas de esa marca cuyo periodo medio de funcionamiento sea superior a 330 días, con probabilidad 0.97.
Calcule el tamaño mínimo de la muestra.
Parte I
Tenemos un cofre A con 2 monedas de oro y 3 de plata, un cofre B con 5 monedas de oro y 4 de plata y un tercer cofre C con 2 monedas de oro. Elegimos un cofre al azar y sacamos una moneda.
a) (1 punto) Calcule la probabilidad de que sea de oro.
b) (1 punto) Sabiendo que ha sido de plata, calcule la probabilidad de que haya sido extraída del cofre A.
Parte II
En los individuos de una población, la cantidad de colesterol en sangre se distribuye según una ley normal de media desconocida y desviación típica de 0,5 g/l. Hemos tomado una muestra de 10 individuos, y se ha obtenido una media muestral de 1,7 g/l.
a) (1 punto) Obtenga un intervalo de confianza, al 95 %, para la cantidad media de colesterol en sangre de la población.
b) (1 punto) ¿Qué nivel de confianza tendría un intervalo para la media cuyos límites fuesen 1,2930 y 2,107?
Parte I
Sean dos sucesos tales que , y . Calcule:
a) (0.5 puntos) y .
b) (0.75 puntos) .
c) (0.75 puntos) . ( indica el contrario del suceso A).
Parte II
Una agencia de alquiler de automóviles necesita estimar el número medio de kilómetros diarios que realiza su flota de automóviles. Se sabe que el número de kilómetros por día sigue una distribución normal con desviación típica de 6 Km/día. Se toman los recorridos de 100 vehículos de la flota, obteniéndose que la media muestral es de 165 Km/día.
a) (1 punto) Construya un intervalo de confianza para la media de dicha distribución a un nivel de confianza del 95 %.
b) (1 punto) ¿Cuál debería ser el tamaño de la muestra para asegurar al nivel de confianza del 90 % que el error cometido es a lo sumo 0.1?
Parte I
En un cineclub hay 80 películas; 60 son de "acción" y 20 de "terror". Susana elige una película al azar y se la lleva. A continuación Luis elige otra película al azar.
a) (1 punto) ¿Cuál es la probabilidad de que tanto Susana como Luis elijan películas de acción?
b) (1 punto) ¿Cuál es la probabilidad de que la película elegida por Luis sea de acción?
Parte II
Se desea estimar, con un error máximo de 0.2 horas, el tiempo medio de estudio diario de los alumnos de primer curso universitario. Se sabe que la desviación típica es de 1 hora y se toma una muestra aleatoria de 100 alumnos.
a) (1 punto) Calcule el nivel de confianza del intervalo que se obtendrá.
b) (1 punto) Calcule el número de individuos que debe tener una muestra para asegurarnos una confianza del 99 %.
Parte I
Dos cajas, A y B, tienen el siguiente contenido:
La A: 5 monedas de 1 euro y 3 de 10 pesetas.
La B: 4 monedas de 1 euro, 4 de 10 pesetas y 2 de 25 pesetas.
De una de las cajas elegida al azar, se extrae una moneda.
a) (1 punto) ¿Cuál es la probabilidad de que sea de 1 euro?
b) (1 punto) Si la moneda extraída resulta ser de 10 pesetas, ¿cuál es la probabilidad de que proceda de la caja B?

Parte II
(2 puntos) Se sospecha que el número de unidades que contiene cada dosis de un medicamento no llega a las 10000 que se indican en el envase. Para comprobar que el contenido medio de las dosis es el indicado tomamos, al azar, 100 dosis y determinamos el número de unidades de cada una, obteniendo de media 9940 unidades y de desviación típica 120 unidades.
¿Qué podemos decir sobre la indicación del envase, para un nivel de confianza del 99 %?
Parte I
La probabilidad de que un jugador A marque un gol de penalti es de 5/6, mientras que la de otro jugador B es 4/5. Si cada uno lanza un penalti,
a) (1 punto) Halle la probabilidad de que marque gol uno solo de los dos jugadores.
b) (1 punto) Halle la probabilidad de que al menos uno marque gol.

Parte II Una muestra aleatoria de 36 cigarrillos de una marca determinada dio un contenido medio de nicotina de 3 miligramos. Se sabe que el contenido en nicotina de estos cigarrillos sigue una distribución normal con una desviación típica de 1 miligramo.
a) (1 punto) ¿Cuál es la probabilidad de que el contenido medio en nicotina de los cigarrillos de esa marca sea superior a 3,2 miligramos?
b) (1 punto) Obtenga un intervalo de confianza al 91% para el contenido medio de nicotina de estos cigarrillos.
Parte I
Dos urnas A y B, que contienen bolas de colores, tienen la siguiente composición:
A: 5 blancas, 3 negras y 2 rojas.
B: 4 blancas y 6 negras.
También tenemos un dado que tiene 4 caras marcadas con la letra A y las otras dos con la letra B. Tiramos el dado y sacamos una bola al azar de la urna que indica el dado.
a) (0.75 puntos) ¿Cuál es la probabilidad de que esa bola sea blanca?
b) (0.5 puntos) ¿Cuál es la probabilidad de que esa bola sea roja?
c) (0.75 puntos) La bola extraída ha resultado ser blanca, ¿cuál es la probabilidad de que proceda de la urna B?

Parte II
Un estudio realizado sobre 100 usuarios revela que un automóvil recorre anualmente un promedio de 15200 Km con una desviación típica de 2250 Km.
a) (1 punto) Determine un intervalo de confianza, al 99 %, para la cantidad promedio de kilómetros recorridos.
b) (1 punto) ¿Cuál debe ser el tamaño mínimo de la muestra para que el error cometido no sea superior a 500 Km, con igual confianza?
Parte I
En el experimento aleatorio de lanzar una moneda tres veces se consideran los siguientes sucesos:
A: "sacar al menos una cara y una cruz".
B: "sacar a lo sumo una cara".
a) (1 punto) Determine el espacio muestral asociado a ese experimento y los sucesos A y B.
b) (1 punto) ¿Son independientes ambos sucesos?

Parte II
(2 puntos) La cantidad de hemoglobina en sangre del hombre sigue una ley normal con desviación típica de 2 g/dl.
Calcule el nivel de confianza de una muestra de 12 extracciones de sangre que indique que la media poblacional de hemoglobina en sangre está entre 13 y 15 gramos por decilitro.
Parte I
Dado un espacio muestral E se consideran los sucesos A y B, cuyas probabilidades son
P(A) = 2/3 y P(B) = 1/2.
a) (0.75 puntos) ¿Pueden ser los sucesos A y B incompatibles? ¿Por qué?
b) (0.75 puntos) Suponiendo que los sucesos A y B son independientes, calcule .
c) (0.5 puntos) Suponiendo que , calcule .

Parte II
(2 puntos) Una ciudad de 2000 habitantes está poblada por personas de pelo negro, rubio o castaño.
Se ha seleccionado, mediante muestreo aleatorio estratificado con afijación proporcional, una muestra constituida por 28 personas de pelo negro, 32 de pelo rubio y 20 de pelo castaño.
Determine cuál es la composición, según el color del pelo, de esa ciudad.
Parte I
El 35 % de los estudiantes de un centro docente practica el fútbol. El 70 % de los que practican el fútbol estudia Matemáticas, así como el 25 % de los que no practican el fútbol.
Calcule la probabilidad de que al elegir, al azar, un estudiante de ese centro:
a) (1 punto) Estudie Matemáticas.
b) (1 punto) Practique el fútbol, sabiendo que no es alumno de Matemáticas.

Parte II
(2 puntos) En una población normal con varianza conocida se ha tomado una muestra de tamaño 49 y se ha calculado su media: .
Determine la varianza de la población sabiendo que el intervalo de confianza, al 95 %, para la media poblacional es (3.64 , 4.76).

Consumo de cigarrrillos diarios	0-5	5-10	10-15	15-20	20-25
Población femenina (miles de hab.)	2	10	15	7	2

Sección 1	Sección 2	Sección 3	Sección 4	Sección 5
500	860	1.200	700	740

Componentes defectuosos	0	1	2	3	4
Nº de juguetes	767	172	50	8	3

nº de caras	0	1	2	3	4	5
nº de series	38	144	342	287	164	25