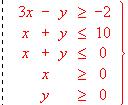
Se pide:
(a) (1 punto) Dibujarlo y hallar sus vértices.
(b) (1 punto) Razonar si es posible maximizar y minimizar en él la función
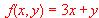
(c) (1 punto) En caso afirmativo, calcular el valor óptimo correspondiente indicando en que puntos se consigue el máximo o el mìnimo.
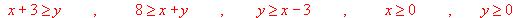
a) (2 puntos) Dibujar la región que definen y calcular sus vértices.
b) (1 punto) Hallar el punto de esa región en el que la función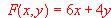 
alcanza el valor máximo y calcular dicho valor.
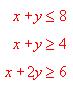
a) (2 puntos) Dibuje la región y determinar sus vértices.
b) (1 punto) Dada la función objetivo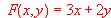 
, halle dónde alcanza dicha función su valor mìnimo y calcule éste.
Se dispone de tierras de abono, pero éstas no contienen ni calcio ni potasio. El agricultor necesita que cada Kg. de tierra de abono tenga al menos 12 unidades de CA y 13 de K. Dispone en el mercado de dos tipo de pastillas A y B cuyos contenidos en unidades de calcio y potasio se dan en el cuadro siguiente:
| Ca | K | |
| A | 2 | 6 |
| B | 4 | 2 |
Sabiendo que cada pastilla de tipo A cuesta 10 pta. y cada una del tipo B, 20 pta. y que no se pueden añadir más de 6 pastillas por Kg. de tierra (ello "quemarìa" la cosecha) ¿Cuantas pastillas de tipo A y de tipo B debe ñadir a cada Kg. de tierra de abono para cumplir los requisitos a un costo mìnimo? ¿Cuánto costarìa producir una tonelada de tierra de abono (sin contar el costo de la tierra)?
Una industria vinìcola produce vino y vinagre. El doble de la producción de vino es siempre menor o igual que la producción de vinagre más cuatro unidades. Por otra parte, el triple de la producción de vinagre sumado con cuatro veces la producción de vino se mantiene siempre menor o igual a 18 unidades. Halle el número de unidades de cada producto que deben producir para alcanzar un beneficio máximo, sabiendo que cada unidad de vino da un beneficio de 800 Pta. y cada unidad de vinagre 200 Pta.
El dueño de una papelerìa dispone de 700 cuadernos, 1.200 bolìgrafos y 1.100 lápices. Desea ponerlos a la venta en lotes de dos tipos, L1 y L2.
Cada lote del tipo L1 está formado por 10 cuadernos, 20 bolìgrafos y 10 lápices, y se venderá a 1.000 Pta. Cada lote L2 está formado por 10 cuadernos, 10 bolìgrafos y 20 lápices, y se venderá a 700 Pta. Calcule:
a) (2 puntos) Cuántos lotes conviene hacer de cada tipo para alcanzar un ingreso máximo.
b) (1 punto) Cuánto dinero se obtendrá por la venta de todos esos lotes.
Un joyero fabrica dos tipos de anillos de boda. Cada anillo del primer tipo requiere 2 gramos de platino y 1 gramo de oro; cada anillo del segundo tipo requiere 1 gramo de platino y 2 gramos de oro.
Los anillos del primer tipo se venden a 6.000 Pta./unidad y los del segundo tipo a 4.000 Pta./unidad. El joyero dispone de 150 gramos de cada metal y desea fabricar anillos de forma que el beneficio que obtenga sea máximo.
a) (1 punto) Plantee el problema y dibuje la región factible.
b) (1 punto) Halle cuántos anillos de cada tipo debe vender el joyero para que obtenga el máximo ingreso.
c) (1 punto) Calcule dicho ingreso.
Una empresa agrìcola necesita almacenar sus dos clases de productos, A y B. Una unidad de producto A ocupa 1,6 m3 y una unidad de producto B ocupa 2,5 m3 , siendo la capacidad total del almacén 1.000 m3 . El precio de una unidad del producto A es de 120 Pta. y el de una unidad del B es de 130 Pta. Calcule cuantas unidades de cada clase deben producirse para que la diferencia entre los ingresos por venta y los gastos por almacenamiento sea máxima, sabiendo que el coste de cada m3 de almacén es de 5 Pta.
Una empresa fabrica dos artìculos, A y B. El artìculo A cuesta 2.000 Pta. y el artìculo B cuesta 1.500 Pta. Se sabe que el número de unidades fabricadas diariamente del artìculo B no supera en 10 unidades a las del artìculo A, y que entre los dos artìculos no se superan diariamente las 30 unidades. También se sabe que la producción del artìculo B no baja diariamente de 10 unidades.
a) (1 punto) Formule el sistema de inecuaciones asociado al enunciado.
b) (1 punto) Dibuje la región factible y determine sus vértices.
c) (1 punto) Halle los costes máximo y mìnimo de la producción diaria.
Cierto taller se dedica a la revisión mecánica y eléctrica de dos marcas de Automóviles (A y B). La revisión de un automóvil de la marca A requiere 1 hora de mecánica y 1 hora de electricidad, siendo el precio de la revisión de 7.000 ptas, y la revisión de un automóvil de marca B requiere 1 hora de mecánica y 2 horas de electricidad, siendo su precio de 10.000 ptas. Teniendo en cuenta el numero de operarios de que dispone el taller, el máximo número de horas al dìa que puede dedicar a las revisiones mecánicas es de 50 hora y las revisiones eléctricas de 70 horas. ¿Cuántos automóviles de cada marca deberá revisar diariamente el taller con objeto de obtener máxima ganancia.
a) (1 punto) Dibuje el recinto limitado por las siguientes inecuaciones:
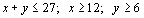
b) (1 punto) Determine los vértices de este recinto.
c) (1 punto) ¿Cuáles son los valores máximo y mínimo de la función F(x,y)=90x+60y en el recinto anterior y en qué puntos alcanza dichos valores?
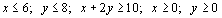
(1 punto) Calcule sus vértices.
(1 punto) Calcule el máximo dela función F(x,y)=20+60y en dicho recinto
Una confitería es famosa por sus dos especialidades en tartas: la tarta Imperial
y la tarta de Lima.
La tarta Imperial requiere para su elaboración medio kilo de azúcar y 8 huevos, y tiene un precio de venta de 1.200 pesetas. La tarta de Lima necesita 1 kilo de azúcar y 8 huevos, y tiene un precio de venta de 1.500 pesetas.
Debido a una mala previsión, se encuentra con la imposibilidad de realizar pedidos de huevos y azúcar, y elaborados ya todos los demás productos que ofertan, les quedan en el almacén 10 kilos de azúcar y 120 huevos para la preparación de las citadas tartas.
a) ¿Qué combinaciones de especialidades puede hacer? Plantear el problema y representar gráficamente el conjunto de soluciones.
b) ¿Cuántas unidades de cada especialidad han de producirse para obtener el mayor ingreso por ventas? ¿A cuánto asciende dicho ingreso?
La región factible de un problema de programación lineal es la intersección del primer cuadrante con los tres semiplanos definidos por las siguientes inecuaciones.
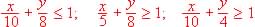
a) Dibuja dicha región y determina sus vértices.
b) Calcula el mínimo de la función objetivo, F(x, y) = 4x + 5y, en el recinto anterior.
En unos grandes almacenes se ha iniciado una campaña de venta de lavadoras y de televisores. Se ha calculado que un vendedor invierte 8 minutos en la venta de una lavadora y 10 en la venta de un televisor, mientras que un instalador dedica 12 minutos a una lavadora y 5 minutos a un televisor. Se dispone de 4 vendedores y 3 instaladores cada uno de los cuales dedica 5 horas diarias a la venta o a la instalación de los electrodomésticos durante los 16 días que dura la campaña. Si se sabe que se obtiene un beneficio de 45.000 pesetas por televisor y de 50.000 pesetas por lavadora vendidos. ¿Cuántas lavadoras y cuántos televisores conviene poner a la venta para obtener máximo beneficio?
Se desea realizar una mezcla con dos sustancias A y B, que ha de contener como mínimo 10 unidades de cada una de ellas. Estas sustancias nos las venden dos
proveedores en forma de lotes.
El lote del primer proveedor es tal que los contenidos de B y A están en la relación de 4 a 1 y contiene una unidad de A.
El lote del segundo proveedor es tal que los contenidos de A y B están en la relación de 4 a 1 y contiene una unidad de B.
El primer proveedor vende cada lote a 1.000 pesetas, precio que es la mitad de a lo que vende el segundo el suyo. Ambos proveedores nos venden lotes enteros o fracciones de ellos.
¿Qué número de lotes hemos de comprar para que el coste sea mínimo? ¿Cuál es
ese coste?
Dibujar la región determinada por las inecuaciones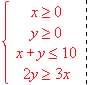 
y maximizar la función f(x, y) = 4x + 3y sometida a las restricciones dadas por estas inecuaciones.
Una fábrica de productos alimenticios elabora patés de dos variedades distintas en envases de 100 gramos de peso neto. Cada envase de la variedad A contiene 80 gramos de hígado de cerdo y 20 gramos de fécula y los de la variedad B, 60
gramos de hígado de cerdo y 40 gramos de fécula. Durante los procesos de elaboración no pueden manipularse más de 240 kilogramos de hígado de cerdo ni más de 100 kilogramos de fécula. Sabiendo que los beneficios por lata son de 30 pesetas (variedad A) y 24 pesetas (variedad B), se pide:
a) Hallar el número de latas que habría que fabricar para obtener un beneficio máximo.
b) ¿Cuál sería dicho beneficio máximo?. Justificar las respuestas.
En una fábrica de maquetas de aviones se construyen dos tipos de maquetas, A y B. La fábrica está dividida en dos salas: una de montaje y otra de acabado.
Para la fabricación de cada modelo A se requieren 3 horas semanales en la sala de montaje y 3 en la de acabado. La fabricación de cada modelo B requiere 5 horas semanales en la sala de montaje y 3 en la de acabado. La sala de montaje puede estar funcionando como máximo 150 horras a la semana, y la de acabado, 120.
Si el beneficio es de 300 dólares en cada modelo A y de 400 en cada modelo B,
¿cuántos modelos de cada tipo habrá que fabricar cada semana para maximizar
los beneficios, suponiendo que se venden todos?
Un artesano fabrica collares y pulseras. Hacer un collar le lleva dos horas y hacer una pulsera una hora. El material de que dispone no le permite hacer más de 50 piezas. Como mucho, el artesano puede dedicar al trabajo 80 horas. Por cada collar gana 500 pesetas y por cada pulsera gana 400 pesetas. El artesano desea determinar el número de collares y pulseras que debe fabricar para optimizar sus beneficios.
a) Exprésense la función objetivo y las restricciones del problema.
b) Represéntese gráficamente el recinto definido.
Obténgase el número de collares y pulseras correspondientes al máximo beneficio.
Una agencia de viajes vende paquetes turísticos para acudir a la final de un campeonato de fútbol. La agencia está considerando ofrecer dos tipos de viajes: El primero de ellos (A) incluye desplazamiento en autocar para dos personas, una noche de alojamiento en habitación doble y cuatro comidas. El segundo (B) incluye desplazamiento en autocar para una persona, una noche de alojamiento (en habitación también doble) y dos comidas.
El precio de venta del paquete A es de 15.000 PTA y el del paquete B es de 9.000 PTA. La agencia tienen contratada un máximo de 30 plazas de autobús, 20 habitaciones dobles y 56 comidas. El número de paquetes del tipo B no debe superar al de los del tipo A. La empresa desea maximizar sus ingresos.
Se pide:
a) Expresa la función objeto.
b) Escribe mediante inecuaciones las restricciones del problema y representa gráficamente el recinto definido.
c) Determina cuántos paquetes de cada tipo debe vender la agencia para que sus ingresos sean máximos. Calcula dichos ingresos.
Los alumnos de un instituto pretenden vender dos tipos de lotes, A y B para sufragarse los gastos del viaje de estudios. Cada lote de tipo A consta de una caja de mantecados y cinco participaciones de lotería, cada lote de tipo B consta de dos cajas de mantecados y dos participaciones de lotería. Por cada lote de tipo A vendido los alumnos obtienen un beneficio de 1.225 pesetas y por cada lote de tipo B de 1.250 pesetas.
a) Determínese la función objetivo y exprésense mediante inecuaciones las restricciones del problema.
b) ¿Cuántas unidades de cada tipo de lote deben vender los alumnos para que el beneficio obtenido sea máximo? Calcúlese dicho beneficio.
Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos. Por necesidades de mercado, es necesario que haya
mayor o igual número de mecánicos que de electricistas y que el número de
mecánicos no supere el doble que el de electricistas. En total hay disponibles
30 electricistas y 20 mecánicos. El beneficio de la empresa por jornada es de
25.000 pesetas por electricista y 20.000 pesetas por mecánico.
¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo
beneficio?
Un orfebre fabrica dos tipos de joyas. La unidad de tipo A se hace con 1 g de oro y 1,5 g de plata y se vende a 4.000 pesetas. La de tipo B se vende a 5.000
pesetas y lleva 1,5 g de oro y 1 g de plata.
Si sólo dispone de 750 g de cada metal, ¿cuántas joyas ha de fabricar de cada tipo
para obtener el máximo beneficio?
En un almacén de frutas hay 800 kg de naranjas, 800 kg de manzanas y 500 kg de plátanos. Para su venta se hacen dos lotes: A y B. El lote A contiene 1 kg de
naranjas, 2 kg de manzanas y 1 kg de plátanos; y el lote B se compone de 2 kg de
naranjas, 1 kg de manzanas y 1 kg de plátanos. El beneficio que se obtiene con el lote
A es de 120 pesetas y, con el lote B, de 140 pesetas.
Determina, justificando las respuestas:
a) El número de lotes de cada clase que se deben formar para conseguir unos beneficios máximos.
b) El valor de dichos beneficios máximos.
Dibújese el recinto que cumple las siguientes restricciones:
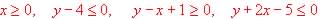
(3 puntos) Cierta sala de espectáculos tiene una capacidad máxima de 1500 personas, entre adultos y niños; el número de niños asistentes no puede superar los 600. El precio de la entrada a una sesión de un adulto es de 800 pts, mientras que la de un niño es de un 40 % menos. El número de adultos no puede superar al doble del número de niños.
Cumpliendo las condiciones anteriores, ¿cuál es la cantidad máxima que se puede recaudar por la venta de entradas? ¿Cuántas de las entradas serán de niños?
(3 puntos) Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar 1600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A cuesta 4 millones de pts y puede transportar 200 personas y 6 toneladas de equipaje; la contratación de uno del tipo B cuesta 1 millón de pts y puede transportar 100 personas y 15 toneladas de equipaje.
¿Cuántos aviones de cada tipo deben utilizarse para que el coste sea mínimo?
a) (1 punto) Represente gráficamente el recinto definido por el siguiente sistema de inecuaciones:
.
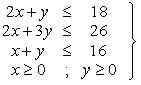b) (1 punto) Calcule los vértices de ese recinto.
c) (1 punto) Obtenga en dicho recinto el valor máximo y el mínimo de la función 
. Diga en que puntos se alcanzan.
Sea el conjunto de restricciones siguiente:
.
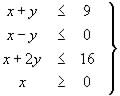a) (1 punto) Dibuje la región factible determinada por dichas restricciones.
b) (1 punto) Calcule los vértices de dicha región.
c) (1 punto) Obtenga los puntos en los que la función objetivo 
presenta el máximo y el mínimo.
(3 puntos) Para fabricar 2 tipos de cable, A y B, que se venderán a 150 y 100 pts el metro, respectivamente, se emplean 16 Kg de plástico y 4 Kg de cobre para cada Hm (hectómetro) del tipo A y 6 Kg de plástico y 12 Kg de cobre para cada Hm del tipo B.
Sabiendo que la longitud de cable fabricado del tipo B no puede ser mayor que el doble de la del tipo A y que, además, no pueden emplearse más de 252 Kg de plástico ni más de 168 Kg de cobre, determine la longitud, en Hm, de cada tipo de cable que debe fabricarse para que la cantidad de dinero obtenida en su venta sea máxima.
Sea el recinto definido por las siguientes inecuaciones:
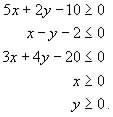
a) (2 puntos) Dibuje dicho recinto y determine sus vértices.
b) (1 punto) Determine en qué punto de ese recinto alcanza la función 
el máximo valor.